ចំនួនថេរត្រីកោណមាត្រពិត

តារាងចំនួនថេរ

0°: មូលដ្ឋានគ្រឹះ

$\sin 0=0\,$

$\cos 0=1\,$

$\tan 0=0\,$

$\cot 0=\infty \,$​មិនកំនត់

3°: ពហុកោណមានជ្រុង៦០

$\sin {\frac {\pi }{60}}=\sin 3^{\circ }={\frac {2(1-{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}+1)}{16}}\,$

$\cos {\frac {\pi }{60}}=\cos 3^{\circ }={\frac {2(1+{\sqrt {3}}){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)({\sqrt {3}}-1)}{16}}\,$

$\tan {\frac {\pi }{60}}=\tan 3^{\circ }={\frac {\left((2-{\sqrt {3}})(3+{\sqrt {5}})-2\right)\left(2-{\sqrt {2(5-{\sqrt {5}})}}\right)}{4}}\,$

$\cot {\frac {\pi }{60}}=\cot 3^{\circ }={\frac {\left((2+{\sqrt {3}})(3+{\sqrt {5}})-2\right)\left(2+{\sqrt {2(5-{\sqrt {5}})}}\right)}{4}}\,$

6°: ពហុកោណមានជ្រុង៣០

$\sin {\frac {\pi }{30}}=\sin 6^{\circ }={\frac {{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1}{8}}\,$

$\cos {\frac {\pi }{30}}=\cos 6^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)}{8}}\,$

$\tan {\frac {\pi }{30}}=\tan 6^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{2}}\,$

$\cot {\frac {\pi }{30}}=\cot 6^{\circ }={\frac {{\sqrt {3}}(3+{\sqrt {5}})+{\sqrt {2(25+11{\sqrt {5}})}}}{2}}\,$

9°: ពហុកោណមានជ្រុង២០

$\sin {\frac {\pi }{20}}=\sin 9^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)-2{\sqrt {5-{\sqrt {5}}}}}{8}}\,$

$\cos {\frac {\pi }{20}}=\cos 9^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)+2{\sqrt {5-{\sqrt {5}}}}}{8}}\,$

$\tan {\frac {\pi }{20}}=\tan 9^{\circ }={\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}\,$

$\cot {\frac {\pi }{20}}=\cot 9^{\circ }={\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}\,$

12°: ពហុកោណមានជ្រុង១៥

$\sin {\frac {\pi }{15}}=\sin 12^{\circ }={\frac {{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{8}}\,$

$\cos {\frac {\pi }{15}}=\cos 12^{\circ }={\frac {{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1}{8}}\,$

$\tan {\frac {\pi }{15}}=\tan 12^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}}{2}}\,$

$\cot {\frac {\pi }{15}}=\cot 12^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)+{\sqrt {2(5+{\sqrt {5}})}}}{2}}\,$

15°: ពហុកោណមានជ្រុង១២

$\sin {\frac {\pi }{12}}=\sin 15^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)}{4}}\,$

$\cos {\frac {\pi }{12}}=\cos 15^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)}{4}}\,$

$\tan {\frac {\pi }{12}}=\tan 15^{\circ }=2-{\sqrt {3}}\,$

$\cot {\frac {\pi }{12}}=\cot 15^{\circ }=2+{\sqrt {3}}\,$

18°: ពហុកោណមានជ្រុង១០

$\sin {\frac {\pi }{10}}=\sin 18^{\circ }={\frac {{\sqrt {5}}-1}{4}}={\frac {\varphi -1}{2}}={\frac {1}{2\varphi }}\,$

$\cos {\frac {\pi }{10}}=\cos 18^{\circ }={\frac {\sqrt {2(5+{\sqrt {5}})}}{4}}\,$

$\tan {\frac {\pi }{10}}=\tan 18^{\circ }={\frac {\sqrt {5(5-2{\sqrt {5}})}}{5}}\,$

$\cot {\frac {\pi }{10}}=\cot 18^{\circ }={\sqrt {5+2{\sqrt {5}}}}\,$

21°: ផលបូក 9° + 12°

$\sin {\frac {7\pi }{60}}=\sin 21^{\circ }={\frac {2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}-{\sqrt {2}}({\sqrt {3}}-1)(1+{\sqrt {5}})}{16}}\,$

$\cos {\frac {7\pi }{60}}=\cos 21^{\circ }={\frac {2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {3}}+1)(1+{\sqrt {5}})}{16}}\,$

$\tan {\frac {7\pi }{60}}=\tan 21^{\circ }={\frac {\left(2-(2+{\sqrt {3}})(3-{\sqrt {5}})\right)\left(2-{\sqrt {2(5+{\sqrt {5}})}}\right)}{4}}\,$

$\cot {\frac {7\pi }{60}}=\cot 21^{\circ }={\frac {\left(2-(2-{\sqrt {3}})(3-{\sqrt {5}})\right)\left(2+{\sqrt {10{\sqrt {5}}}}\right)}{4}}\,$

22.5°: ពហុកោណមានជ្រុង៨

$\sin {\frac {\pi }{8}}=\sin 22.5^{\circ }={\frac {\sqrt {2-{\sqrt {2}}}}{2}}\,$

$\cos {\frac {\pi }{8}}=\cos 22.5^{\circ }={\frac {\sqrt {2+{\sqrt {2}}}}{2}}\,$

$\tan {\frac {\pi }{8}}=\tan 22.5^{\circ }={\sqrt {2}}-1\,$

$\cot {\frac {\pi }{8}}=\cot 22.5^{\circ }={\sqrt {2}}+1\,$

24°: ផលបូល 12° + 12°

$\sin {\frac {2\pi }{15}}=\sin 24^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2}}{\sqrt {5-{\sqrt {5}}}}}{8}}\,$

$\cos {\frac {2\pi }{15}}=\cos 24^{\circ }={\frac {{\sqrt {6}}{\sqrt {5-{\sqrt {5}}}}+{\sqrt {5}}+1}{8}}\,$

$\tan {\frac {2\pi }{15}}=\tan 24^{\circ }={\frac {{\sqrt {50+22{\sqrt {5}}}}-{\sqrt {3}}(3+{\sqrt {5}})}{2}}\,$

$\cot {\frac {2\pi }{15}}=\cot 24^{\circ }={\frac {{\sqrt {2}}{\sqrt {5-{\sqrt {5}}}}+{\sqrt {3}}({\sqrt {5}}-1)}{2}}\,$

27°: ផលបូក 12° + 15°

$\sin {\frac {3\pi }{20}}=\sin 27^{\circ }={\frac {({\sqrt {5}}+1){\sqrt {5+{\sqrt {5}}}}-{\sqrt {2}}({\sqrt {5}}-1)}{8}}\,$

$\cos {\frac {3\pi }{20}}=\cos 27^{\circ }={\frac {({\sqrt {5}}+1){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {5}}-1)}{8}}\,$

$\tan {\frac {3\pi }{20}}=\tan 27^{\circ }={\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}\,$

$\cot {\frac {3\pi }{20}}=\cot 27^{\circ }={\sqrt {5}}-1+{\sqrt {5-2{\sqrt {5}}}}\,$

30°:ពហុកោណមានជ្រុង៦

$\sin {\frac {\pi }{6}}=\sin 30^{\circ }={\frac {1}{2}}\,$

$\cos {\frac {\pi }{6}}=\cos 30^{\circ }={\frac {\sqrt {3}}{2}}\,$

$\tan {\frac {\pi }{6}}=\tan 30^{\circ }={\frac {\sqrt {3}}{3}}\,$

$\cot {\frac {\pi }{6}}=\cot 30^{\circ }={\sqrt {3}}\,$

33°: ផលបូក 15° + 18°

$\sin {\frac {11\pi }{60}}=\sin 33^{\circ }={\frac {2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}(1+{\sqrt {3}})({\sqrt {5}}-1)}{16}}\,$

$\cos {\frac {11\pi }{60}}=\cos 33^{\circ }={\frac {2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}(1-{\sqrt {3}})({\sqrt {5}}-1)}{16}}\,$

$\tan {\frac {11\pi }{60}}=\tan 33^{\circ }={\frac {\left(2-(2-{\sqrt {3}})(3+{\sqrt {5}})\right)\left(2+{\sqrt {2(5-{\sqrt {5}})}}\right)}{4}}\,$

$\cot {\frac {11\pi }{60}}=\cot 33^{\circ }={\frac {\left(2-(2+{\sqrt {3}})(3+{\sqrt {5}})\right)\left(2-{\sqrt {2(5-{\sqrt {5}})}}\right)}{4}}\,$

36°: ពហុកោណមានជ្រុង៥

$\sin {\frac {\pi }{5}}=\sin 36^{\circ }={\frac {\sqrt {2(5-{\sqrt {5}})}}{4}}\,$

$\cos {\frac {\pi }{5}}=\cos 36^{\circ }={\frac {1+{\sqrt {5}}}{4}}={\frac {\varphi }{2}}\,$

$\tan {\frac {\pi }{5}}=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}\,$

$\cot {\frac {\pi }{5}}=\cot 36^{\circ }={\frac {\sqrt {5(5+2{\sqrt {5}})}}{5}}\,$

39°: ផលបូក 18°+ 21°

$\sin {\frac {13\pi }{60}}=\sin 39^{\circ }={\frac {2(1-{\sqrt {3}}){\sqrt {5-{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)}{16}}\,$

$\cos {\frac {13\pi }{60}}=\cos 39^{\circ }={\frac {2(1+{\sqrt {3}}){\sqrt {5-{\sqrt {5}}}}+{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)}{16}}\,$

$\tan {\frac {13\pi }{60}}=\tan 39^{\circ }={\frac {\left((2-{\sqrt {3}})(3-{\sqrt {5}})-2\right)\left(2-{\sqrt {2(5+{\sqrt {5}})}}\right)}{4}}\,$

$\cot {\frac {13\pi }{60}}=\cot 39^{\circ }={\frac {\left((2+{\sqrt {3}})(3-{\sqrt {5}})-2\right)\left(2+{\sqrt {2(5+{\sqrt {5}})}}\right)}{4}}\,$

42°: ផលបូក 21° + 21°

$\sin {\frac {7\pi }{30}}=\sin 42^{\circ }={\frac {{\sqrt {6}}{\sqrt {5+{\sqrt {5}}}}-{\sqrt {5}}+1}{8}}\,$

$\cos {\frac {7\pi }{30}}=\cos 42^{\circ }={\frac {{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}+{\sqrt {3}}({\sqrt {5}}-1)}{8}}\,$

$\tan {\frac {7\pi }{30}}=\tan 42^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}}{2}}\,$

$\cot {\frac {7\pi }{30}}=\cot 42^{\circ }={\frac {{\sqrt {2(25-11{\sqrt {5}})}}+{\sqrt {3}}(3-{\sqrt {5}})}{2}}\,$

45°: ការេ

$\sin {\frac {\pi }{4}}=\sin 45^{\circ }={\frac {\sqrt {2}}{2}}\,$

$\cos {\frac {\pi }{4}}=\cos 45^{\circ }={\frac {\sqrt {2}}{2}}\,$

$\tan {\frac {\pi }{4}}=\tan 45^{\circ }=1\,$

$\cot {\frac {\pi }{4}}=\cot 45^{\circ }=1\,$

60°: ត្រីកោណ

$\sin {\frac {\pi }{3}}=\sin 60^{\circ }={\frac {\sqrt {3}}{2}}\,$

$\cos {\frac {\pi }{3}}=\cos 60^{\circ }={\frac {1}{2}}\,$

$\tan {\frac {\pi }{3}}=\tan 60^{\circ }={\sqrt {3}}\,$

$\cot {\frac {\pi }{3}}=\cot 60^{\circ }={\frac {\sqrt {3}}{3}}\,$

ចំនាំ

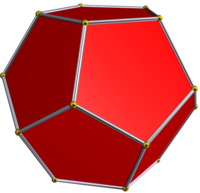
ការប្រើប្រាស់ចំពោះចំនួនថេរ

មាឌនៃសូលីតដែលបង្កើតដោយពហុកោណមានជ្រុង៥(បញ្ចកោណ) ហើយ $a\,$ ជាប្រវែងនៃជ្រុងរបស់បញ្ចកោណ

សំដែងដោយ

$V={\frac {5a^{3}\cos {36^{\circ }}}{\tan ^{2}{36^{\circ }}}}$

ដោយប្រើ

$\cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}}\,$

$\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}\,$

វាក្លាយទៅជា

$V={\frac {a^{3}(15+7{\sqrt {5}})}{4}}\,$