សមីការដឺក្រេទី១
សមីការដឺក្រេទី១ ឬ សមីការលីនេអ៊ែ (អង់គ្លេស: linear equation, បារាំង: équation linéaire) គឺជាសមីការពិជគណិតមួយដែលតួនីមួយៗជាចំនួនថេរ ឬជាផលគុណនៃចំនួនថេរមួយនឹងអថេរមួយ(អថេរដែលមិនមានស្វ័យគុណ)។ សមីការដឺក្រេទី១ អាចមានអថេរមួយ ឬ ច្រើន។ ទំរង់ទូទៅនៃសមីការដឺក្រេទី១ដែលមានអថេរ២ គឺ និង សំដែងដោយ
ដែល m និង b ជាចំនួនថេរ ហើយមានអថេរ x និង y ដែលyជាធម្មតាគេសរសេរមានមេគុណ១នៅពីរមុខ ។ ចំលើយនៃសមីការនេះមានសំនុំចំលើយបង្កើតបានជាបន្ទាត់ត្រង់មួយនៅក្នុងប្លង់។ ចំនួនថេរ m ជាមេគុណប្រាប់ទិសនៃបន្ទាត់ ហើយចំនួនថេរ b ជាតំលៃនៃចំនុចដែលបន្ទាត់កាត់អ័ក្ស(y'oy)។
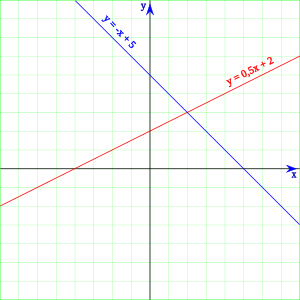
ទម្រង់ របស់សមីការដឺក្រេទ១នៅក្នុងប្លង់
[កែប្រែ]| ផ្នែកនេះទទេ។ អ្នកអាចជួយបានដោយបន្ថែមព័ត៌មាន។ |
ទំរង់ទូទៅ
[កែប្រែ]ដែល A និង B មិនស្មើសូន្យ ។ បើ A មិនសូន្យ នោះអាប់ស៊ីសនៃចំនុចដែលជាប្រសព្វរវាងបន្ទាត់និងអ័ក្សអាប់ស៊ីស គឺ −C/A។ បើ B មិនសូន្យ នោះអរដោនេនៃចំនុចដែលជាប្រសព្វរវាងបន្ទាត់និងអ័ក្សអរដោនេ គឺ −C/B ហើយមេគុណប្រាប់ទិសនៃបន្ទាត់គឺ −A/B។
ទំរង់ស្តង់ដា
[កែប្រែ]- ដែល A និង B មិនសូន្យ។[១]
ទំរង់ដែលមានមេគុណប្រាប់ទិស និង ចំនុចកាត់អ័ក្ស
[កែប្រែ]រូបមន្តចំពោះអ័ក្សអរដោនេ
[កែប្រែ]ដែល m ជាមេគុណប្រាប់ទិសនៃបន្ទាត់ ហើយ b ជាអរដោនេនៃចំនុចប្រសព្វរវាងបន្ទាត់និងអ័ក្សអរដោនេ។ បើគេអោយ នោះគេទទួលបាន ។
រូបមន្តចំពោះអ័ក្សអាប់ស៊ីស
[កែប្រែ]ដែល m ខុសពីសូន្យជាមេគុណប្រាប់ទិសនៃបន្ទាត់ ហើយ c ជាអាប់ស៊ីសនៃចំនុចប្រសព្វរវាងបន្ទាត់និងអ័ក្សអាប់ស៊ីស។ បើគេអោយ នោះគេបាន ។
ទំរង់ចំពោះចំនុចនិងមេគុណប្រាប់ទិស
[កែប្រែ]ដែល m ជាមេគុណប្រាប់ទិសនៃបន្ទាត់ ហើយ (x1,y1) ជាចំនុចនៅលើបន្ទាត់ ។ គេបាន ។
ទំរង់ចំពោះចំនុចប្រសព្វ
[កែប្រែ]ដែល c និង b មិនសូន្យ ។ ក្រាបនៃសមីការមានc ជាអាប់ស៊ីសនៃចំនុចដែលបន្ទាត់កាត់អ័ក្សអាប់ស៊ីស និង bជាអរដោនេនៃចំនុចដែលបន្ទាត់កាត់អ័ក្សអរដោនេ។ ទំរង់នេះអាចត្រូវគេបំលែងទៅជាទំរង់ស្តង់ដា ដោយយក A = 1/c, B = 1/b និង C = 1។
ទំរង់ចំពោះពីរចំនុច
[កែប្រែ]ដែល p ≠ h ។ ក្រាបកាត់តាមចំនុច (h,k) និង (p,q) ហើយមានមេគុណប្រាប់ទិស m = (q−k) / (p−h) ។
ទំរង់ប៉ារ៉ាមែត្រ
[កែប្រែ]- និង
ប្រព័ន្ធសមីការទាំងពីរមានប៉ារ៉ាមែត t រួមជាមួយមេគុណប្រាប់ទិស m = V / T ចំនុចប្រសព្វរវាងបន្ទាត់និងអ័ក្សអាប់ស៊ីស (VU−WT) / V និងចំនុចប្រសព្វរវាងបន្ទាត់និងអ័ក្សអរដោនេ (WT−VU) / T ។
នេះអាចទាក់ទងជាមួយទំរង់ចំពោះពីរចំនុច ដែល T = p−h, U = h, V = q−k, និង W = k
- និង
ក្នុងករណីនេះ t ប្រែប្រួពី ០ ត្រង់ចំនុច(h,k) ទៅ ១ ត្រង់ចំនុច (p,q) ។
ករណីពិសេស
[កែប្រែ]នេះជាករណីពិសេសនៃទំរង់ស្តង់ដាដែល A = 0 និង B = 1 ឬ ទំរង់ចំពោះចំនុចនិងមេគុណប្រាប់ទិសដែល m = 0 ។ ក្រាបគឺជាបន្ទាត់កាត់អ័ក្សអរដោនេត្រង់ចំនុចដែលមានអរដោនេ b ហើយស្របនឹងអ័ក្សអាប់ស៊ីស។
នេះជាករណីពិសេសនៃទំរង់ស្តង់ដាដែល 'A = 1 និង B = 0 ។ ក្រាបគឺជាបន្ទាត់ឈរកាត់អ័ក្សអាប់ស៊ីសត្រង់ចំនុចដែលមានអាប់ស៊ីស c ហើយស្របនឹងអ័ក្សអរដោនេ។
ទំនាក់ទំនងរវាងអនុគមន៍លីនេអ៊ែនិងប្រមាណវិធី
[កែប្រែ]ក្នុងករណីពិសេសដែលបន្ទាត់កាត់តាមគល់អ័ក្ស ប្រសិនបើអនុគមន៍លីនេអ៊ែត្រូវគេសរសេរក្នុងទំរង់ y = f(x) នោះ f មានលក្ខណៈ
និង
ដែល a ជាចំនួនស្កាលែរ(ចំនួនថេរ) ។ អនុគមន៍ដែលផ្ទៀងផ្ទាត់នឹងលក្ខណៈនេះ គេហៅថាអនុគមន៍លីនេអ៊ែ។ អនុគមន៍លីនេអ៊ែត្រូវគេឃើញជារើយៗនៅក្នុងគណិតវិទ្យាអនុវត្តន៍។
សមីការដឺក្រេទី១(សមីការលីនេអ៊ែ)ដែលមានអថេរច្រើនជាង២
[កែប្រែ]សមីការដឺក្រេទ១អាចត្រូវគេសំដែងដោយភ្ជាប់នឹងអថេរច្រើនជាង២។ សមីការទូទៅនៃសមីការដឺក្រេទ១ដែលមាន n អថេរសំដែងដោយ
ក្នុងសមីការនេះ a1, a2, …, an គឺជាមេគុណ x1, x2, …, xn គឺជាអថេរ និង b ជាចំនួនថេរ។ នៅពេលអនុវត្តជាមួយអថេរ៣ឬច្រើន ជាទូទៅគេជំនួស x 1ដោយ x , x2 ដោយ y និង x3 ដោយ z .............។
សមីការនេះ ដំណាងអោយប្លង់ដែលមានតំរុយ(n–1) នៅក្នុងលំហអឺគ្លីត(Euclidean space) តំរុយ n (ឧទាហរណ៍ ប្លង់នៅក្នុងលំហ៣)។
កំណត់ចំណាំ
[កែប្រែ]- ↑ Barnett, Ziegler & Byleen 2008, pg. 15
ឯកសារយោង
[កែប្រែ]- Barnett, R.A.; Ziegler, M.R.; Byleen, K.E. (2008), College Mathematics for Business, Economics, Life Sciences and the Social Sciences (11th រ.រ.), Upper Saddle River, N.J.: Pearson, ល.ស.ប.អ. 0-13-157225-3
តំណភ្ជាប់ខាងក្រៅ
[កែប្រែ]- Algebraic Equations at EqWorld: The World of Mathematical Equations.
- [១] Archived 2011-06-29 at the វេយប៊ែខ ម៉ាស៊ីន. Video tutorial on solving one step to multistep equations
- Linear Equations and Inequalities Archived 2014-11-15 at the វេយប៊ែខ ម៉ាស៊ីន. Open Elementary Algebra textbook chapter on linear equations and inequalities.























