ទ្រឹស្តីបទប្រាម៉ាហ្គឹបតា

$\overline{BD}\perp\overline{AC}$ និង $\overline{EF}\perp\overline{BC}$

$\Rightarrow |\overline{AF}|=|\overline{FD}|$

ក្នុងធរណីមាត្រ ទ្រឹស្តីបទប្រាម៉ាហ្គឹបតា (Brahmagupta theorem) ផ្តល់នូវលក្ខខណ្ឌចាំបាច់​ក្នុងករណីអង្កត់ទ្រូង​ទាំងពីរនៃ​ចតុកោណចារឹកក្នុងរង្វង់កែងគ្នា។

ទ្រឹស្តីបទ

ប្រសិនបើអង្កត់ទ្រូងទាំងពីរនៃចតុកោណចារឹកក្នុងរង្វង់កែងគ្នា គេបានគ្រប់អង្កត់កែងទៅនឹងជ្រុងមួយនៃចតុកោណគូសកាត់ចំនុចប្រសព្វ​នៃអង្កត់ទ្រូង​ទៅកាន់ជ្រុងឈមរបស់វា តែងតែចែក​ជ្រុងឈមនោះ​ជាពីរអង្កត់មានរង្វាស់ស្មើគ្នាជានិច្ច។

ទ្រឹស្តីបទនេះត្រូវដាក់ឈ្មោះថាទ្រឹស្តីបទប្រាម៉ាហ្គឹបតា ដោយផ្តល់កិត្តិយសដល់គណិតវិទូជនជាតិឥណ្ឌាឈ្មោះ ប្រាម៉ាហ្គឹបតា (Brahmagupta) ។

ការពិពណ៌នាបន្ថែម៖ តាង A B C និង D ជាបួនចំនុចនៅលើរង្វង់ ដែលបន្ទាត់ (AC) និង (BD) កែងគ្នា។ តាង M ជាចំនុចប្រសព្វរវាង AC និង BD ។ គូសទំលាក់ចំនោលកែងពី M មកលើបន្ទាត់ (BC) តាងដោយ E ។ តាង F ជាចំនុចប្រសព្វជាចំនុចប្រសព្វនៃបន្ទាត់ (EM) និង (AD) ។ នោះគេបានទ្រឹស្តីបទពោលថា F ជាចំនុចកណ្តាលនៃ AD ។

សំរាយបញ្ជាក់

បំណកស្រាយទ្រឹស្តីបទ

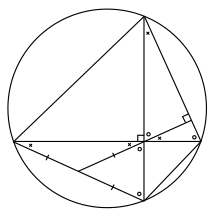
យើងចាំបាច់ត្រូវបង្ហាញថា $AF = FD \,$ ។ យើងនឹងបង្ហាញថា AF និង FD ពិតជាស្មើនឹង FM ។

ដើម្បីបង្ហាញថា $AF = FM \,$ ដំបូងយើងកត់សំគាល់ឃើញថា

$\angle FAM = \angle CBM$ (ព្រោះវាជាមុំចារឹកក្នុងដែលស្កាត់ដោយធ្នូដូចគ្នានៃរង្វង់)

ម្យ៉ាងទៀត $\angle CBM \,$ និង$\angle CME \,$ ជាមុំបន្ថែមនៃមុំ $\angle BCM \,$ (មុំដែលមានផលបូកធំជាង $\pi \,$)

$\angle AMF = \angle EMC = \angle MBC = \angle MAD$

គេបានមុំ $\angle ME =\angle FMA \,$

ហេតុនេះត្រីកោណ AFM គឺជាត្រីកោណសមបាត ។ ដូចនេះ $AF = FM \, \qquad \color{magenta} (i)$ ។

ដូចគ្នាដែរចំពោះសំរាយបញ្ជាក់ថា $FD = FM \,$ ។

$\angle AMF = \angle EMC = \angle MBC = \angle MAD$

គេបានត្រីកោណ DFM ជាត្រីកោណសមបាត ដែល $FD = FM \, \qquad \color{magenta} (ii)$ ។

តាម $\color{magenta} (i)$ និង $\color{magenta} (ii)$ គេបាន $AF = FD \,$ ។

ដូចនេះសំរាយបញ្ជាក់ត្រូវនឹងពំនោលនៃទ្រឹស្តីបទ។

សូមមើលផងដែរ

• រូបមន្តប្រាម៉ាហ្គឹបតា (Brahmagupta's formula)
• ប្រាម៉ាហ្គឹបតា (គណិតវិទូជនជាតិឥណ្ឌា)