បន្ទាត់ (ធរណីមាត្រ)
បន្ទាត់ចំនួន គឺជាខ្សែកោងត្រង់មានប្រវែងមិនកំនត់និងមានចំនុចរាប់មិនអស់។ បន្ទាត់អាចត្រូវគេបង្កើតតាមរយះពីរចំនុចផ្សេងគ្នា។
នៅក្នុងប្លង់ (វិមាត្រពីរ ឬ តំរុយពីរ) បន្ទាត់អាចស្រប ឬ កាត់គ្នាត្រង់មួយចំនុច។ នៅក្នុងលំហ (វិមាត្រ៣ឬច្រើន ឬ តំរុយ៣ឬច្រើន) បន្ទាត់អាចស្រប ឬ មិនស្របតែមិនកាត់គ្នា (មិនអាចបង្កើតបានប្លង់មួយ) ឬ កាត់គ្នាត្រង់មួយចំនុច។
ឧទាហរណ៍
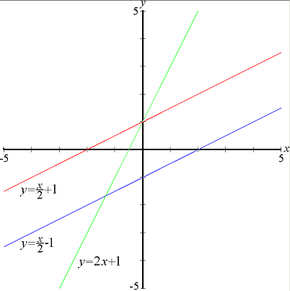
[កែប្រែ]នៅក្នុងតំរុយដេកាត បន្ទាត់ត្រូគេសំដែងដោយសមីការលីនេអ៊ែរ (សមីការដឺក្រេទី១) និង អនុគមន៍លីនេអ៊ែរ ។ នៅក្នុងប្លង់ (វិមាត្រ២ ឬ តំរុយ២) សមីការទូទៅរបស់បន្ទាត់ គឺ
ដែល
- m ជាមេគុណប្រាប់ទិសរបស់បន្ទាត់។
- x ជាអថេរ។
នៅក្នុងលំហ (វិមាត្រ៣) បន្ទាត់មួយត្រូវគេសំដែងដោយសមីការប៉ារ៉ាម៉ែត្រ
ដែល
- x0, y0, និង z0 តំលៃដើមនៃ : x, y, និង z ។
- a, b, និង c ជាធាតុរបស់វ៉ិចទ័រប្រាប់ទិសនៃបន្ទាត់ (វ៉ិចទ័រ(a, b, c) ស្របនឹងបន្ទាត់)។
លក្ខណះ
[កែប្រែ]នៅក្នុងតំរុយ២ ដូចជាប្លង់ បន្ទាត់ពីរផ្សេងគ្នាត្រូវតែ ស្រប ឬ កាត់គ្នាត្រង់ចំនុចមួយ។ តែនៅក្នុងលំហដែលមានតំរុយច្រើន បន្ទាត់ទាំងពីរអាចមិន ស្រប ឬ កាត់គ្នា។
នៅក្នុង R2(តំរុយពីរ) បន្ទាត់ L សំដែងដោយ សមីការលីនេអ៊ែរ
ដែល
a និង b មិនសូន្យ។
អង្កត់
[កែប្រែ][[сделайте нормальный язык]គឺជាផ្នែកមួយនៃបន្ទាត់។





