អាំងតេក្រាលត្រីកោណមាត្រ

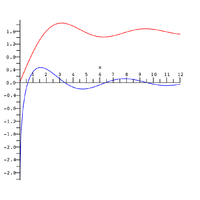
Si(x) (ក្រហម) and Ci(x) (ខៀវ)

ក្នុងគណិតវិទ្យា អាំងតេក្រាលត្រីកោណមាត្រ(trigonometric integrals) គឺជាគ្រួសារនៃអាំងតេក្រាលដែលទាក់ទងនឹងអនុគមន៍ត្រីកោណមាត្រ។ អាំងតេក្រាលត្រីកោណមាត្រគ្រឹះមួយចំនួន ត្រូវបានពិភាក្សានៅក្នុងតារាងអាំងតេក្រាលនៃអនុគមន៍ត្រីកោណមាត្រ ។

អាំងតេក្រាលស៊ីនុស

និយមន័យអាំតេក្រាលស៊ីនុសផ្សេងគ្នា គឺ

${\rm {Si}}(x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt$

${\rm {si}}(x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt$

${\rm {Si}}(x)\,$ គឺជាព្រីមីទីវនៃ$\sin x/x\,$ ដែលសូន្យចំពោះ $x=0\,$

${\rm {si}}(x)\,$ គឺជាព្រីមីទីវនៃ$\sin x/x\,$ ដែលសូន្យចំពោះ $x=\infty$

យើងបាន

${\rm {si}}(x)={\rm {Si}}(x)-{\frac {\pi }{2}}$

ចំនាំ ៖ ${\frac {\sin t}{t}}$ គឺជាអនុគមន៍ស៊ីនុសកាឌីណាល់(sinc function) ហើយនិង អនុគមន៍បេស៊ែលស្វែរទីសូន្យ(the zeroth spherical Bessel function) ។

អាំងតេក្រាលកូស៊ីនុស

និយមន័យអាំតេក្រាលកូស៊ីនុសផ្សេងគ្នា គឺ

${\rm {Ci}}(x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cos t-1}{t}}\,dt$

${\rm {ci}}(x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt$

${\rm {Cin}}(x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt$

${\rm {ci}}(x)\,$ គឺជាព្រីមីទីវនៃ $\cos x/x\,$ ដែលសូន្យចំពោះ $x=\infty$ ។

យើងបាន

${\rm {ci}}(x)={\rm {Ci}}(x)\,$

${\rm {Cin}}(x)=\gamma +\ln x-{\rm {Ci}}(x)\,$

អាំងតេក្រាលស៊ីនុសអ៊ីពែបូលីក

អាំងតេក្រាស៊ីនុសអ៊ីពែបូលីក:

${\rm {Shi}}(x)=\int _{0}^{x}{\frac {\sinh t}{t}}\,dt={\rm {shi}}(x).$

អាំងតេក្រាលកូស៊ីនុសអ៊ីពែបូលីក

អាំងតេក្រាលកូស៊ីនុសអ៊ីពែបូលីក:

${\rm {Chi}}(x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt={\rm {chi}}(x)$

ដែល $\gamma$ គឺជាចំនួនថេរអឺលែរ-ម៉ាសឆេរ៉ូនី(Euler-Mascheroni constant)​ ។

ពន្លាត

ពន្លាតជាច្រើនអាចត្រូវគេប្រើ ដើម្បីកំនត់តំលៃនៃអាំងតេក្រាលត្រីកោណមាត្រ ដោយផ្អែកលើតំលៃអាគុយម៉ង់ ។

ស៊េរីអាស៊ីមតូត (ចំពោះអាគុយម៉ង់ធំ)

${\rm {Si}}(x)={\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+...\right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+...\right)$

${\rm {Ci}}(x)={\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+...\right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+...\right)$

ស៊េរីនេះគឺមិនទាល់(divergent) បើទោះបីជាអាចត្រូវគេប្រើ សំរាប់ប៉ាន់ស្មានតំលៃពិតប្រាកដត្រង់ $~{\rm {Re}}(x)\gg 1~$ ។

ស៊េរីទាល់(Convergent series)

${\rm {Si}}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots$

${\rm {Ci}}(x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots$

ស៊េរីទាំងនេះទាល់ត្រង់គ្រប់ $~x~$ បើទោះបីចំពោះ​ $|x|\gg 1$ ការកំនត់តំលៃគឺយឺត និងមិនត្រឹមត្រូវ​ បើនៅគ្រប់ចំនុចទាំងអស់។

ទំនាក់ទំនងជាមួយអាំងតេក្រាលអិចស្ប៉ូណង់ស្យែលនៃអាគុយម៉ង់និម្មិត

អនុគមន៍ ${\rm {E}}_{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}{\rm {d}}t~~,~~~~({\rm {Re}}(z)\geq 0)$ គឺត្រូវបានគេហៅថា អាំងតេក្រាលអិចស្ប៉ូណង់ស្យែល ។ វាមានទំនាក់ទំនងយ៉ាងជិតស្និតនឹង Si និង Ci:

${\rm {E}}_{1}({\rm {i}}\!~x)=-{\frac {\pi }{2}}+{\rm {Si}}(x)-{\rm {i}}\cdot {\rm {Ci}}(x)~~~~,~~~~~(x>0)$

ដោយ អនុគមន៍ដែលទាក់ទងនីមួយៗគឺជាវិភាគ លើកលែងតែផ្នែកដែលត្រូវគេកាត់ត្រង់តំលៃអវិជ្ជមាននៃអាគុយម៉ង់ ផ្ទៃនៃសុពលភាពនៃទំនាក់ទំនង គឺអាចមានដល់ ${\rm {Re}}(x)>0$ ។ (ក្រៅពីតំលៃនេះ តួបន្ថែមដែលជាកត្តាអាំងតេក្រាលនៃ $\pi$ លេចចេញក្នុងកន្សោម)។