ក្នុងគណិតវិទ្យា អនុគមន៍ត្រីកោណមាត្រ ជាអនុគមន៍ នៃមុំ ។ អនុគមន៍ត្រីកោណមាត្រមានសារសំខាន់ក្នុងការសិក្សាអំពីត្រីកោណ រង្វង់ និងម៉ូដែលនៃបាតុភូតដែលមានលក្ខណៈជាខួប។ អនុគមន៍ត្រីកោណមាត្រជាធម្មតាកំនត់ដោយផលធៀប រវាងជ្រុងពីរនៃត្រីកោណកែង ជាមួយនឹងមុំនៃត្រីកោណនោះ និង អាចកំនត់ដោយសមមូលនឹងប្រវែងនៃអង្កត់ខុសគ្នានៅលើរង្វង់ត្រីកោណមាត្រ ។ វាក៏អាចត្រូវបានគេសំដែងវាជាស៊េរីអនន្ត ឬ ជាចំលើយនៃសមីការឌីផេរ៉ង់ស្យែល ។
ក្នុងការប្រើប្រាស់ មានអនុគមន៍ត្រីកោណមាត្រគ្រឹះចំនួន៦គឺ
ស៊ីនុស (sin)
កូស៊ីនុស (cos)
តង់សង់ (tan ឬ tg)
កូតង់សង់ (cot ឬ cotan)
សេកង់ (sec)
កូសេកង់ (csc ឬ cosec) .
ស៊ីនុស កូស៊ីនុស និង តង់សង់ គឺត្រូវបានគេប្រើប្រាស់ច្រើនជាងគេ។ អនុគមន៍សេកង់ និង កូសេកង់គឺកំរនឹងត្រូវបានគេប្រើណាស់។
ចំពោះសេចក្តីលំអិតអំពីរូបមន្តត្រីកោណមាត្រ សូមមើលតារាងរូបមន្តត្រីកោណមាត្រ ។
[ កែប្រែ ] ផលធៀបត្រីកោណមាត្រ ជាផលធៀបរវាង ជ្រុងឈមនៃមុំនោះនឹង អ៊ីប៉ូតេនុស។
អនុគមន៍
អក្សរបំព្រួញ
រូបមន្ត
រូបត្រីកោណកែង
ស៊ីនុស
sin
sin
θ
=
B
C
C
A
{\displaystyle \sin \theta ={BC \over CA}}
កូស៊ីនុស
cos
cos
θ
=
A
B
C
A
{\displaystyle \cos \theta ={AB \over CA}}
តង់សង់
tan ឬ tg
tan
θ
=
B
C
A
B
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={BC \over AB}={\sin \theta \over \cos \theta }}
សេកង់
sec
sec
θ
=
C
A
A
B
=
1
cos
θ
{\displaystyle \sec \theta ={CA \over AB}={1 \over \cos \theta }}
កូសេកង់
csc ឬ cosec
csc
θ
=
C
A
B
C
=
1
sin
θ
{\displaystyle \csc \theta ={CA \over BC}={1 \over \sin \theta }}
កូតង់សង់
cot ឬ cotan
cot
θ
=
A
B
B
C
=
csc
θ
sec
θ
=
1
tan
θ
{\displaystyle \cot \theta ={AB \over BC}={\csc \theta \over \sec \theta }={1 \over \tan \theta }}
ការយល់ដឹងថាមានមាត្រដ្ឋានមួយចំនួនទាក់ទងរវាងជ្រុងនៃត្រីកោណ និងមុំ នៃត្រីកោណគឺត្រូវបានគេស្គាល់ថាត្រីកោណដូចគ្នានៅរក្សាតំលៃផលធៀបរវាងជ្រុងរបស់ពួកវាដដែល។ មានន័យថា ចំពោះត្រីកោណដូចគ្នា ផលធៀបនៃអ៊ីប៉ូតេនុស និងជ្រុងផ្សេងទៀតនៅរក្សាតំលៃដដែល។ អនុគមន៍ត្រីកោណមាត្រគឺសំដែងជាផលធៀបទាំងនេះ។
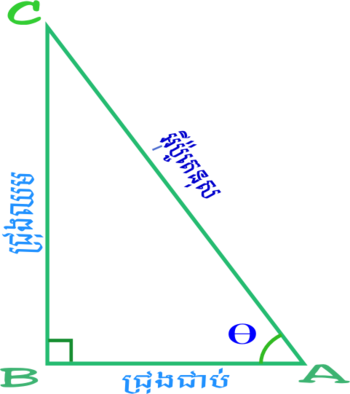
ដើម្បីកំនត់និយមន័យនៃអនុគមន៍ត្រីកោណមាត្រចំពោះមុំ A (ក្នុងរូបមុំត្រង់កំពូល A គឺមុំ
θ
{\displaystyle \ \theta }
ត្រីកោណកែង ដែលមានមុំ A ជាមុំកែង។ យើងប្រើប្រាស់ឈ្មោះខាងក្រោមចំពោះជ្រុងទាំងបីនៃត្រីកោណ ៖
អ៊ីប៉ូតេនុស គឺជាជ្រុងឈមនឹងមុំកែង ឬ ត្រូវបានគេអោយនិយមន័យថាគឺជាជ្រុងដែលវែងជាងគេនៃត្រីកោណកែង ។ជ្រុងឈមគឺជាជ្រុងដែលឈមនឹងមុំដែលយើងកំនត់ (ក្នុងរូបមុំដែលកំនត់គឺមុំ A ដូចនេះជ្រុងឈមនឹងមុំ A គឺជ្រុង BC) ។
ជ្រុងជាប់គឺជាជ្រុងដែលជាប់នឹងមុំដែលយើងកំនត់ និង ជាជ្រុងជាប់នឹងមុំកែង (ក្នុងរូបជ្រុងជាប់នៃមុំ A គឺជ្រុង AB) ។ គ្រប់ត្រីកោណ គឺត្រូវបានកំនត់ក្នុងប្លង់អឺគ្លីត ហេតុដូចនេះផលបូកមុំផ្នែកខាងក្នុងនៃត្រីកោណនិមួយៗគឺស្មើនឹង ១៨០ ដឺក្រេ (
π
{\displaystyle \ \pi }
រ៉ាដ្យង់ ) ។ ដូចនេះចំពោះត្រីកោណកែងមុំមិនកែងពីរគឺស្ថិតនៅចន្លោះពី ០ ទៅ ៩០ដឺក្រេ (
π
2
{\displaystyle \ {\frac {\pi }{2}}}
រ៉ាដ្យង់ ) ។ និយមន័យខាងក្រោមគឺកំនត់មុំពី ០ ទៅ ៩០ដឺក្រេ។ យើងអាចបន្លាយវាចំពោះគ្រប់សំនុំនៃអាគុយម៉ង់ពិតដោយប្រើរង្វង់ត្រីកោណមាត្រ ឬ ដោយប្រើលក្ខណៈស៊ីមេទ្រី ព្រោះវាជាអនុគមន៍ខួប ។
ត្រីកោណកែងត្រង់ B យើងតាង
អ៊ីប៉ូតេនុស (AC) ដោយ
h
{\displaystyle \ h}
ជ្រុងឈម (BC) ដោយ
a
{\displaystyle \ a}
ជ្រុងជាប់ (AB) ដោយ
c
{\displaystyle \ c}
ដូចបង្ហាញក្នុងរូប។
ស៊ីនុសនៃមុំមួយគឺជាផលធៀបរវាងរង្វាស់ប្រវែងនៃជ្រុងឈម និង រង្វាស់អ៊ីប៉ូតេនុស។ គេបាន
sin
A
=
B
C
A
C
=
a
h
{\displaystyle \ \sin A={\frac {BC}{AC}}={\frac {a}{h}}}
ចូរកត់សំគាល់ថាផលធៀបនេះមិនអាស្រ័យនឹងទំហំនៃត្រីកោណកែងដែលជ្រើសរើសទេ ដរាបណាវាមានមុំ A ដោយសារគ្រប់ត្រីកោណបែបនេះគឺជាត្រីកោណដូចគ្នា។
កូស៊ីនុសនៃមុំមួយគឺជាផលធៀបរវាងរង្វាស់ជ្រុងជាប់និងរង្វាស់អ៊ីប៉ូតេនុស ។ គេបាន
cos
A
=
A
B
A
C
=
c
h
{\displaystyle \ \cos A={\frac {AB}{AC}}={\frac {c}{h}}}
តង់សង់នៃមុំគឺជាផលធៀបរវាងជ្រុងឈមនិងជ្រុងជាប់។ គេបាន
tan
A
=
B
C
A
B
=
a
c
{\displaystyle \ \tan A={\frac {BC}{AB}}={\frac {a}{c}}}
កូតង់សង់នៃមុំ A (cot A) គឺជាចំរាស់នៃតង់សង់នៃមុំ A ( tan A) ។ មានន័យថាវាជាផលធៀបរវាងជ្រុងជាប់និងជ្រុងឈម។
cot
A
=
1
tan
A
=
A
B
B
C
=
c
a
{\displaystyle \ \cot A={\frac {1}{\tan A}}={\frac {AB}{BC}}={\frac {c}{a}}}
សេកង់នៃមុំ A (sec A) គឺជាចំរាស់នៃកូស៊ីនុសនៃមុំ A (cos A) ។ មានន័យថាវាជាផលធៀបរវាងអ៊ីប៉ូតេនុសនិងជ្រុងជាប់។
sec
A
=
1
cos
A
=
A
C
A
B
=
h
c
{\displaystyle \ \sec A={\frac {1}{\cos A}}={\frac {AC}{AB}}={\frac {h}{c}}}
កូសេកង់នៃមុំ A (cosec A ឬ csc A) គឺជាចំរាស់នៃស៊ីនុសនៃមុំ A ។ មានន័យថាវាជាផលធៀបរវាងអ៊ីប៉ូតេនុសនិងជ្រុងឈម។
csc
A
=
1
sin
A
=
A
C
B
C
=
h
a
{\displaystyle \ \csc A={\frac {1}{\sin A}}={\frac {AC}{BC}}={\frac {h}{a}}}
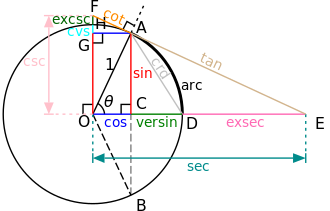
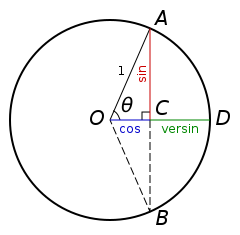
រង្វង់ត្រីកោណមាត្រ អនុគមន៍ត្រីកោណមាត្រគ្រឹះទាំង៦អាចត្រូវបានកំនត់ពីរង្វង់ត្រីកោណមាត្រ ដែលជារង្វង់ មានកាំ មានរង្វាស់ស្មើនឹង១ និង មានផ្ចិត ស្ថិតនៅត្រង់គល់ O ។ និយមន័យនៃរង្វង់ត្រីកោណមាត្រផ្តល់នូវវិធីសាស្រ្តមួយចំនួនក្នុងការគណនា។ រង្វង់ត្រីកោណមាត្រអាចកំនត់នូវអនុគមន៍ត្រីកោណមាត្រចំពោះគ្រប់មុំ (អាគុយម៉ង់ )វិជ្ជមានឬអវិជ្ជមាន មិនតែចំពោះមុំនៅចន្លោះពី ០ ទៅ ៩០ ដឺក្រេ (០ និង
π
2
{\displaystyle \ {\frac {\pi }{2}}}
ក្នុងប្លង់ដេកាត នៃតំរុយអរតូណរមេ
(
O
;
i
→
,
j
→
)
{\displaystyle (O;{\vec {i}},{\vec {j}})}
រង្វង់ត្រីកោណមាត្រ គឺជារង្វង់ ផ្ចិត O និងកាំ ស្មើនឹង ១។ ប្រសិនបើយើងចាត់ទុកចំនុច A(xA , yA ) ជាចំនុចនៅលើរង្វង់ គេបាន
cos
(
i
→
,
O
A
→
)
^
=
x
A
{\displaystyle \cos {\widehat {({\vec {i}},{\vec {OA}})}}=x_{A}}
sin
(
i
→
,
O
A
→
)
^
=
y
A
{\displaystyle \sin {\widehat {({\vec {i}},{\vec {OA}})}}=y_{A}}
ពីទ្រឹស្តីបទពីតាករ សមីការរង្វង់ត្រីកោណមាត្រគឺ
x
2
+
y
2
=
1
{\displaystyle \ x^{2}+y^{2}=1}
ពីទ្រឹស្តីបទពីតាករ វាផ្តល់នូវទំនាក់ទំនង
cos
2
(
θ
)
+
sin
2
(
θ
)
=
1
{\displaystyle \cos ^{2}(\theta )+\sin ^{2}(\theta )=1\,}
ក្នុងរូបមុំមួយចំនួនត្រូវបានអោយគិតជារ៉ាដ្យង់ ។ រង្វាស់មុំ ក្នុងទិសដៅស្របនឹងទ្រនិចនាឡិកាគឺជាមុំវិជ្ជមាន និង រង្វាស់មុំក្នុងទិសដៅផ្ទុយពីទ្រនិចនាឡិកាគឺជាមុំអវិជ្ជមាន។ តាងបន្ទាត់ មួយកាត់តាមគល់តំរុយ បង្កើតបានមុំ
θ
{\displaystyle \ \theta }
រង្វង់ត្រីកោណមាត្រ ។ កូអរដោនេ x និង y នៃចំនុចប្រព្វនេះគឺស្មើនឹង
cos
θ
{\displaystyle \ \cos \theta }
sin
θ
{\displaystyle \ \sin \theta }
ត្រីកោណ ក្នុងក្រាភិកបង្កើតបានរូបមន្ត៖ កាំ គឺស្មើនឹងអ៊ីប៉ូតេនុស និង មានរង្វាស់ស្មើនឹង ១ ហេតុនេះយើងបាន
sin
θ
=
y
1
{\displaystyle \ \sin \theta ={\frac {y}{1}}}
cos
θ
=
x
1
{\displaystyle \ \cos \theta ={\frac {x}{1}}}
ចំពោះមុំដែលធំជាង
2
π
{\displaystyle \ 2\pi }
−
2
π
{\displaystyle \ -2\pi }
2
π
{\displaystyle \ 2\pi }
sin
θ
=
sin
(
θ
+
2
π
k
)
{\displaystyle \sin \theta =\sin \left(\theta +2\pi k\right)\,}
cos
θ
=
cos
(
θ
+
2
π
k
)
{\displaystyle \cos \theta =\cos \left(\theta +2\pi k\right)\,}
ចំពោះគ្រប់មុំ
θ
{\displaystyle \ \theta }
ខួបវិជ្ជមានតូចបំផុតនៃអនុគមន៍ខួប គឺត្រូវបានគេហៅថាខួបព្រីមីទីវ ឬ ខួប នៃអនុគមន៍ ។ ខួបព្រីមីទីវនៃស៊ីនុស កូស៊ីនុស សេកង់ ឬ កូសេកង់ គឺជារង្វង់ពេញ (មួយជុំរង្វង់) មានន័យថាខួបរបស់វាមានតំលៃ
2
π
{\displaystyle \ 2\pi }
π
{\displaystyle \ \pi }
tan
θ
=
sin
θ
cos
θ
,
sec
θ
=
1
cos
θ
,
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}\,,\quad \sec \theta ={\frac {1}{\cos \theta }}\,,}
csc
θ
=
1
sin
θ
,
cot
θ
=
cos
θ
sin
θ
{\displaystyle \csc \theta ={\frac {1}{\sin \theta }}\,,\quad \cot \theta ={\frac {\cos \theta }{\sin \theta }}\,}
រង្វង់ត្រីកោណមាត្រ ។
θ
{\displaystyle \ \theta }
រ៉ាដ្យង់ ។ អនុគមន៍សេកង់និងតង់សង់ស្ថិតនៅលើបន្ទាត់ ឈរហើយនឹង និង អនុគមន៍ស៊ីនុសស្ថិតនៅលើបន្ទាត់មានចលនា ។ (ពាក្យនឹង នៅទីនេះមានន័យថាមិនមានចលនាទៅតាមតំលៃនៃ
θ
{\displaystyle \ \theta }
មានចលនា មានន័យថាអាស្រ័យនឹង
θ
{\displaystyle \ \theta }
θ
{\displaystyle \ \theta }
sin
θ
{\displaystyle \ \sin \theta }
tan
θ
{\displaystyle \ \tan \theta }
∞
{\displaystyle \ \infty }
sec
θ
{\displaystyle \ \sec \theta }
ធរណីមាត្រ នៅលើរង្វង់ត្រីកោណមាត្រ ។ អនុគមន៍ដែលឈ្មោះវាផ្តើមដោយបុព្វបទ កូ ប្រើបន្ទាត់ដេក និង ក្រៅពីនេះប្រើបន្ទាត់ឈរ។
ក្រាបនៃអនុគមន៍ស៊ីនុស និង កូស៊ីនុសក្នុងប្លង់ដេកាត
ក្រាបនៃអនុគមន៍ស៊ីនុស
ក្រាបនៃអនុគមន៍កូស៊ីនុស
ក្រាបនៃអនុគមន៍តង់សង់
ស៊ីនុស , កូស៊ីនុស , តង់សង់ , កូតង់សង់(dotted) , សេកង់(dotted) , កូតង់សង់(dotted)
ស៊ីនុសគឺជាអនុគមន៍សេស :
∀
x
∈
R
{\displaystyle \forall x\in \mathbb {R} }
sin
(
−
x
)
=
−
sin
(
x
)
{\displaystyle \sin(-x)=-\sin(x)\,\!}
កូស៊ីនុសគឺជាអនុគមន៍គូ :
∀
x
∈
R
{\displaystyle \forall x\in \mathbb {R} }
cos
(
−
x
)
=
cos
(
x
)
{\displaystyle \cos(-x)=\cos(x)\,\!}
តង់សង់គឺជាអនុគមន៍សេស :
∀
x
∈
R
∖
{
π
2
+
k
π
,
k
∈
Z
}
{\displaystyle \forall x\in \mathbb {R} \setminus \left\{{\frac {\pi }{2}}+k\pi ,\,k\in \mathbb {Z} \right\}}
tan
(
−
x
)
=
−
tan
(
x
)
{\displaystyle \tan(-x)=-\tan(x)\,\!}
អនុគមន៍ស៊ីនុស (ខៀវ) ខិតជិតពហុធាតេល័រ ដឺក្រ៧ (ពណ៌ផ្កាឈូក) ចំពោះរង្វង់ពេញ (មួយជុំរង្វង់) ដែលមានផ្ចិតត្រង់គល់ O ដោយប្រើតែធរណីមាត្រ និងលក្ខណៈនៃលីមីត វាអាចត្រូវបានគេបង្ហាញថាដេរីវេ នៃស៊ីនុសគឺជាកូស៊ីនុស និង ដេរីវេនៃកូស៊ីនុសគឺស៊ីនុសអវិជ្ជមាន។ ក្នុងគណិតវិទ្យាវិភាគទូទៅ គ្រប់រង្វាស់មុំត្រូវបានគេគិតជារ៉ាដ្យង់ ។ ដោយប្រើទ្រឹស្តីនៃស៊េរីតេល័រ ចំពោះគ្រប់ចំនួនពិត x គេបាន
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\\end{aligned}}}
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
{\displaystyle {\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}\end{aligned}}}
ស៊េរីហ្វួរា (Fourier series)) ពីព្រោះទ្រឹស្តីនៃស៊េរីអនន្ត អាចត្រូវបានគេអភិវឌ្ឍចេញពីមូលដ្ឋានគ្រឹះនៃប្រព័ន្ធចំនួនពិត (real number system) ដោយមិនទាក់ទងនឹងគំនិតបែបធរណីមាត្រណាមួយទេ។ ភាពមានដេរីវេ និង ភាពជាប់នៃអនុគមន៍ទាំងនេះត្រូវបានគេបង្កើតចេញពីនិយមន័យនៃស៊េរីតែឯង។
tan
x
=
∑
n
=
1
∞
(
−
1
)
n
−
1
2
2
n
(
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
=
x
+
x
3
3
+
2
x
5
15
+
17
x
7
315
+
⋯
{\displaystyle {\begin{aligned}\tan x&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+\cdots \end{aligned}}}
ចំពោះ
|
x
|
<
π
2
{\displaystyle |x|<{\frac {\pi }{2}}\,}
csc
x
=
∑
n
=
0
∞
(
−
1
)
n
+
1
2
(
2
2
n
−
1
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
=
1
x
+
x
6
+
7
x
3
360
+
31
x
5
15120
+
⋯
{\displaystyle {\begin{aligned}\csc x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}+{\frac {x}{6}}+{\frac {7x^{3}}{360}}+{\frac {31x^{5}}{15120}}+\cdots \end{aligned}}}
ចំពោះ
0
<
|
x
|
<
π
{\displaystyle 0<|x|<\pi \,}
sec
x
=
∑
n
=
0
∞
U
2
n
x
2
n
(
2
n
)
!
=
∑
n
=
0
∞
(
−
1
)
n
E
2
n
x
2
n
(
2
n
)
!
=
1
+
x
2
2
+
5
x
4
24
+
61
x
6
720
+
⋯
{\displaystyle {\begin{aligned}\sec x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\\&{}=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+{\frac {61x^{6}}{720}}+\cdots \end{aligned}}}
ចំពោះ
|
x
|
<
π
2
{\displaystyle |x|<{\frac {\pi }{2}}\,}
cot
x
=
∑
n
=
0
∞
(
−
1
)
n
2
2
n
B
2
n
x
2
n
−
1
(
2
n
)
!
=
1
x
−
x
3
−
x
3
45
−
2
x
5
945
−
⋯
{\displaystyle {\begin{aligned}\cot x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-\cdots \end{aligned}}}
ចំពោះ
0
<
|
x
|
<
π
{\displaystyle 0<|x|<\pi \,}
ដែល
[ កែប្រែ ] គេអាចស្រាយបញ្ជាក់ដោយចេញពីនិយមន័យស៊េរីដែលអនុគមន៍ស៊ីនុសនិងកូស៊ីនុសគឺជាផ្នែកនិម្មិត និងផ្នែកពិត រៀងគ្នានៃអនុគមន៍អិចស្ប៉ូណង់ស្យែលកុំផ្លិច នៅពេលដែលអាគុយម៉ង់របស់វាជាចំនួននិម្មិតសុទ្ធ។
e
i
θ
=
cos
θ
+
i
sin
θ
{\displaystyle e^{i\theta }=\cos \theta +i\sin \theta \,}
រូបមន្តនេះត្រូវបានគេហៅថារូបមន្តអយល័រ ។ ក្នុងករណីនេះអនុគមន៍ត្រីកោណមាត្រក្លាយជាផ្នែកមួយដ៏មានសារសំខាន់ក្នុងតំណាងធរណីមាត្រនៃចំនួនកុំផ្លិចវិភាគ។ ឧទាហរណ៍៖ ជាមួយនឹងរូបមន្តនេះប្រសិនបើរង្វង់ត្រីកោណមាត្រត្រូវបានគេចាត់ទុកថានៅក្នុងប្លង់កុំផ្លិច កំនត់ដោយ
e
i
x
{\displaystyle \ e^{ix}}
លើសពីនេះទៅទៀត រូបមន្តអយល័រអាចអោយយើងកំនត់និយមន័យនៃអនុគមន៍ត្រីកោណមាត្រចំពោះ អាគុយម៉ង់កុំផ្លិច
z
{\displaystyle \ z}
sin
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
=
e
i
z
−
e
−
i
z
2
i
=
−
i
sinh
(
i
z
)
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\,=\,{e^{iz}-e^{-iz} \over 2i}=-i\sinh \left(iz\right)\,}
cos
z
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
z
2
n
=
e
i
z
+
e
−
i
z
2
=
cosh
(
i
z
)
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\,=\,{e^{iz}+e^{-iz} \over 2}=\cosh \left(iz\right)\,}
ដែល
i
2
=
−
1
{\displaystyle \ i^{2}=-1}
x
{\displaystyle \ x}
cos
x
=
Re
(
e
i
x
)
{\displaystyle \cos x={\mbox{Re }}(e^{ix})\,}
sin
x
=
Im
(
e
i
x
)
{\displaystyle \sin x={\mbox{Im }}(e^{ix})\,}
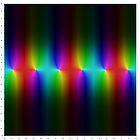
[ កែប្រែ ] ក្នុងក្រាបខាងក្រោមគឺស្ថិតនៅក្នុងដែននៃប្លង់កុំផ្លិច និងតំលៃជាជួររបស់វាត្រូវបានបង្ហាញនៅត្រង់ចំនុចនិមួយៗដោយពណ៌។ ពណ៌ភ្លឺច្បាស់បង្ហាញពីទំហំ (តំលៃដាច់ខាត ) នៃតំលៃជាជួរជាមួយពណ៌ខ្មៅជាតំលៃសូន្យ។ ពណ៌លាំៗបង្ហាញពីបំរែបំរួលនៃអាគុយម៉ង់ ឬ មុំ ដែលត្រូវបានគេវាស់ពីអ័ក្សពិតផ្នែកវិជ្ជមាន។ (ព័ត៌មានបន្ថែម ) ។
ក្រាបនៃអនុគមន៍ត្រីកោណមាត្រក្នុងប្លង់កុំផ្លិច
sin
z
{\displaystyle \sin z\,}
cos
z
{\displaystyle \cos z\,}
tan
z
{\displaystyle \tan z\,}
cot
z
{\displaystyle \cot z\,}
sec
z
{\displaystyle \sec z\,}
csc
z
{\displaystyle \csc z\,}
សញ្ញានៃអនុគមន៍ត្រីកោណមាត្រគឺអាស្រ័យនឹងកាដ្រង់ ក្នុងរង្វង់ត្រីកោណមាត្រ ។ ខាងក្រោមនេះជាតារាងសញ្ញានៃអនុគមន៍ទាំងនេះក្នុងកាដ្រង់ I II III និង IV នៃរង្វង់ត្រីកោណមាត្រ។
កាដ្រង់
sin និង csc
cos និង sec
tan និង cot
I
+
+
+
II
+
−
−
III
−
−
+
IV
−
+
−
ខាងក្រោមនេះជាតារាងរូបមន្តបំលែងនៃអនុគមន៍ត្រីកោណមាត្រនិមួយៗ។
sin
cos
tan
cot
sec
csc
sin(x)
sin
(
x
)
{\displaystyle \,\sin(x)}
1
−
cos
2
(
x
)
{\displaystyle {\sqrt {1-\cos ^{2}(x)}}}
tan
(
x
)
1
+
tan
2
(
x
)
{\displaystyle {\frac {\tan(x)}{\sqrt {1+\tan ^{2}(x)}}}}
1
cot
2
(
x
)
+
1
{\displaystyle {\frac {1}{\sqrt {\cot ^{2}(x)+1}}}}
sec
2
(
x
)
−
1
sec
(
x
)
{\displaystyle {\frac {\sqrt {\sec ^{2}(x)-1}}{\sec(x)}}}
1
csc
(
x
)
{\displaystyle {\frac {1}{\csc(x)}}}
cos(x)
1
−
sin
2
(
x
)
{\displaystyle \,{\sqrt {1-\sin ^{2}(x)}}}
cos
(
x
)
{\displaystyle \,\cos(x)}
1
1
+
tan
2
(
x
)
{\displaystyle \,{\frac {1}{\sqrt {1+\tan ^{2}(x)}}}}
cot
(
x
)
cot
2
(
x
)
+
1
{\displaystyle \,{\frac {\cot(x)}{\sqrt {\cot ^{2}(x)+1}}}}
1
sec
(
x
)
{\displaystyle \,{\frac {1}{\sec(x)}}}
csc
2
(
x
)
−
1
csc
(
x
)
{\displaystyle \,{\frac {\sqrt {\csc ^{2}(x)-1}}{\csc(x)}}}
tan(x)
sin
(
x
)
1
−
sin
2
(
x
)
{\displaystyle \,{\frac {\sin(x)}{\sqrt {1-\sin ^{2}(x)}}}}
1
−
cos
2
(
x
)
cos
(
x
)
{\displaystyle \,{\frac {\sqrt {1-\cos ^{2}(x)}}{\cos(x)}}}
tan
(
x
)
{\displaystyle \,\tan(x)}
1
cot
(
x
)
{\displaystyle \,{\frac {1}{\cot(x)}}}
sec
2
(
x
)
−
1
{\displaystyle \,{\sqrt {\sec ^{2}(x)-1}}}
1
csc
2
(
x
)
−
1
{\displaystyle \,{\frac {1}{\sqrt {\csc ^{2}(x)-1}}}}
cot(x)
1
−
sin
2
(
x
)
sin
(
x
)
{\displaystyle \,{\frac {\sqrt {1-\sin ^{2}(x)}}{\sin(x)}}}
cos
(
x
)
1
−
cos
2
(
x
)
{\displaystyle \,{\frac {\cos(x)}{\sqrt {1-\cos ^{2}(x)}}}}
1
tan
(
x
)
{\displaystyle \,{\frac {1}{\tan(x)}}}
cot
(
x
)
{\displaystyle \,\cot(x)}
1
sec
2
(
x
)
−
1
{\displaystyle \,{\frac {1}{\sqrt {\sec ^{2}(x)-1}}}}
csc
2
(
x
)
−
1
{\displaystyle \,{\sqrt {\csc ^{2}(x)-1}}}
sec(x)
1
1
−
sin
2
(
x
)
{\displaystyle \,{\frac {1}{\sqrt {1-\sin ^{2}(x)}}}}
1
cos
(
x
)
{\displaystyle \,{\frac {1}{\cos(x)}}}
1
+
tan
2
(
x
)
{\displaystyle \,{\sqrt {1+\tan ^{2}(x)}}}
cot
2
(
x
)
+
1
cot
(
x
)
{\displaystyle \,{\frac {\sqrt {\cot ^{2}(x)+1}}{\cot(x)}}}
sec
(
x
)
{\displaystyle \,\sec(x)}
csc
(
x
)
csc
2
(
x
)
−
1
{\displaystyle \,{\frac {\csc(x)}{\sqrt {\csc ^{2}(x)-1}}}}
csc(x)
1
sin
(
x
)
{\displaystyle \,{\frac {1}{\sin(x)}}}
1
1
−
cos
2
(
x
)
{\displaystyle \,{\frac {1}{\sqrt {1-\cos ^{2}(x)}}}}
1
+
tan
2
(
x
)
tan
(
x
)
{\displaystyle \,{\frac {\sqrt {1+\tan ^{2}(x)}}{\tan(x)}}}
cot
2
(
x
)
+
1
{\displaystyle \,{\sqrt {\cot ^{2}(x)+1}}}
sec
(
x
)
sec
2
(
x
)
−
1
{\displaystyle \,{\frac {\sec(x)}{\sqrt {\sec ^{2}(x)-1}}}}
csc
(
x
)
{\displaystyle \,\csc(x)}
[ កែប្រែ ] ខាងក្រោមនេះជាតារាងដេរីវេ និងអាំងតេក្រាល នៃអនុគមន៍ត្រីកោណមាត្រគ្រឹះទាំង៦។ ចំពោះដេរីវេ និង អាំងតេក្រាលនៃអនុគមន៍ត្រីកោណមាត្រទូទៅ សូមមើល តារាងដេរីវេ តារាងអាំងតេក្រាល តារាងអាំងតេក្រាលនៃអនុគមន៍ត្រីកោណមាត្រ ។
អនុគមន៍ (
f
(
x
)
{\displaystyle \ \ f(x)}
ដេរីវេ (
d
d
x
f
(
x
)
{\displaystyle {\frac {d}{dx}}f(x)}
អាំងតេក្រាល (
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx}
sin
x
{\displaystyle \,\ \sin x}
cos
x
{\displaystyle \,\ \cos x}
−
cos
x
+
C
{\displaystyle \,\ -\cos x+C}
cos
x
{\displaystyle \,\ \cos x}
−
sin
x
{\displaystyle \,\ -\sin x}
sin
x
+
C
{\displaystyle \,\ \sin x+C}
tan
x
{\displaystyle \,\ \tan x}
sec
2
x
{\displaystyle \,\ \sec ^{2}x}
−
ln
|
cos
x
|
+
C
{\displaystyle -\ln \left|\cos x\right|+C}
cot
x
{\displaystyle \,\ \cot x}
−
csc
2
x
{\displaystyle \,\ -\csc ^{2}x}
ln
|
sin
x
|
+
C
{\displaystyle \ln \left|\sin x\right|+C}
sec
x
{\displaystyle \,\ \sec x}
sec
x
tan
x
{\displaystyle \,\ \sec {x}\tan {x}}
ln
|
sec
x
+
tan
x
|
+
C
{\displaystyle \ln \left|\sec x+\tan x\right|+C}
csc
x
{\displaystyle \,\ \csc x}
−
csc
x
cot
x
{\displaystyle \,\ -\csc {x}\cot {x}}
−
ln
|
csc
x
+
cot
x
|
+
C
{\displaystyle -\ln \left|\csc x+\cot x\right|+C}
[ កែប្រែ ] [ កែប្រែ ]
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )=\sin \alpha \,\cos \beta +\cos \alpha \,\sin \beta }
sin
(
α
−
β
)
=
sin
α
cos
β
−
cos
α
sin
β
{\displaystyle \sin(\alpha -\beta )=\sin \alpha \,\cos \beta -\cos \alpha \,\sin \beta }
cos
(
α
+
β
)
=
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle \cos(\alpha +\beta )=\cos \alpha \,\cos \beta -\sin \alpha \,\sin \beta }
cos
(
α
−
β
)
=
cos
α
cos
β
+
sin
α
sin
β
{\displaystyle \cos(\alpha -\beta )=\cos \alpha \,\cos \beta +\sin \alpha \,\sin \beta }
tan
(
α
+
β
)
=
tan
α
+
tan
β
1
−
tan
α
tan
β
{\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \,\tan \beta }}}
tan
(
α
−
β
)
=
tan
α
−
tan
β
1
+
tan
α
tan
β
{\displaystyle \tan(\alpha -\beta )={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \,\tan \beta }}}
[ កែប្រែ ] ការគណនានៃអនុគមន៍ត្រីកោណមាត្រគឺជាមុខវិជ្ជាដ៏ស៊ាំញ៉ាំមួយដែលសព្វថ្ងៃការគណនាដោយមនុស្សអាចជៀសវៀងបាន ដោយសារតែការរីកចំរើននៃបច្ចេកវិទ្យាកុំព្យូទ័រ និង ម៉ាស៊ីនគណនាតាមបែបវិទ្យាសាស្រ្តដែលអាចអោយយើងធ្វើការគណនាអនុគមន៍ត្រីកោណមាត្រចំពោះមុំនៅត្រង់តំលៃណាមួយ។ ក្នុងផ្នែកនេះយើងនឹងរៀបរាប់លំអិតអំពីការគណនាក្នុងបរិបទសំខាន់ៗចំនួនបីគឺ៖ បំរើបំរាស់តារាងត្រីកោណមាត្រតាំងពីបុរាណ បច្ចេកវិជ្ជាទំនើបដែលប្រើដោយកុំព្យ័ទ័រ និង មុំសំខាន់ៗមួយចំនួនដែលជាតំលៃពិតធម្មតាងាយស្រួលរក។
ជំហានដំបូងក្នុងការគណនាអនុគមន៍ត្រីកោណមាត្រគឺប្រើការកាត់បន្ថយចន្លោះមុំ ក្នុងចន្លោះតូចគឺពី ០ ទៅ
π
2
{\displaystyle \ {\frac {\pi }{2}}}
ដំបូងឡើយចំពោះកុំព្យូទ័រ មនុស្សបានគិតតំលៃប្រហែលៗនៃអនុគមន៍ត្រីកោណមាត្រដោយការកែខៃពីតារាងលំអិតនៃតំលៃរបស់ពួកវា បានគណនាចំពោះរូបសំខាន់ៗជាច្រើន។ តារាងបែបនេះមានអាចធ្វើបាន ដរាបណាអនុគមន៍ត្រីកោណមាត្រត្រូវគេបញ្ជាក់ប្រាប់ និង ត្រូវបានបង្កើតដោយការអនុវត្តន៍សារចុះសារឡើងនៃកន្លះមុំ និង រូបមន្តមុំបន្ថែមចាប់ពីតំលៃដែលគេស្គាល់ (ឧទាហរណ៍ដូចជា
sin
π
2
=
1
{\displaystyle \ \sin {\frac {\pi }{2}}=1}
កុំព្យូទ័រសម័យទំនើបប្រើប្រាស់បច្ចេកទេសផ្សេងៗគ្នាក្នុងការគណនា។ វិធិសាស្រ្តទូទៅគឺដោយផ្សំពហុធា ឬ ការប៉ានប្រមានសនិទានជាមួយការកាត់បន្ថយចន្លោះមុំ និង ការមើលតារាង ដោយមើលមុំដែលជិតជាងគេក្នុងតារាង បន្ទាប់មកប្រើពហុធា ដើម្បីគណនា។
ចំពោះការគណនាអោយជាក់លាក់ក្នុងកំរិតខ្ពស់បំផុត អនុគមន៍ត្រីកោណមាត្រអាចប៉ាន់តំលៃប្រហែលដោយមធ្យមនព្វន្ធ-ធរណីមាត្រ ។
ចុងក្រោយចំពោះមុំធម្មតាមួយចំនួន តំលៃនៃអនុគមន៍ត្រីកោណមាត្រអាចគណនាបានយ៉ាងងាយដោយដៃដោយប្រើទ្រឹស្តីបទពីតាករ ដូចឧទាហរណ៍ខាងក្រោម។ តាមពិតស៊ីនុស កូស៊ីនុស និង តង់សង់ នៃមុំជាចំនួនគត់
π
60
{\displaystyle \ {\frac {\pi }{60}}}
០ ) អាចគណនាដោយដៃ។
ឧទាហរណ៍៖ គេមានត្រីកោណកែងដែលមុំពីរទៀតមានតំលៃស្មើគ្នា គឺមុំទាំងពីរស្មើនឹង
π
4
{\displaystyle \ {\frac {\pi }{4}}}
π
4
{\displaystyle \ {\frac {\pi }{4}}}
០ ) អាចគណនាដោយប្រើទ្រឹស្តីបទពីតាករ ។
c
=
a
2
+
b
2
=
2
{\displaystyle \ c={\sqrt {a^{2}+b^{2}}}={\sqrt {2}}}
ហេតុនេះ
sin
(
π
/
4
)
=
sin
(
45
∘
)
=
cos
(
π
/
4
)
=
cos
(
45
∘
)
=
1
2
{\displaystyle \sin \left(\pi /4\right)=\sin \left(45^{\circ }\right)=\cos \left(\pi /4\right)=\cos \left(45^{\circ }\right)={1 \over {\sqrt {2}}}\,}
tan
(
π
/
4
)
=
tan
(
45
∘
)
=
sin
(
π
/
4
)
cos
(
π
/
4
)
=
1
2
⋅
2
1
=
2
2
=
1
{\displaystyle \tan \left(\pi /4\right)=\tan \left(45^{\circ }\right)={{\sin \left(\pi /4\right)} \over {\cos \left(\pi /4\right)}}={1 \over {\sqrt {2}}}\cdot {{\sqrt {2}} \over 1}={{\sqrt {2}} \over {\sqrt {2}}}=1\,}
ដើម្បីកំនត់អនុគមន៍ត្រីកោណមាត្រចំពោះមុំ
π
3
{\displaystyle \ {\frac {\pi }{3}}}
π
6
{\displaystyle \ {\frac {\pi }{6}}}
ត្រីកោណសម័ង្ស គឺ
π
3
{\displaystyle \ {\frac {\pi }{3}}}
ត្រីកោណកែង ដែលមានមុំមួយស្មើនឹង
π
6
{\displaystyle \ {\frac {\pi }{6}}}
π
3
{\displaystyle \ {\frac {\pi }{3}}}
1
2
{\displaystyle \ {\frac {1}{2}}}
3
2
{\displaystyle \ {\frac {\sqrt {3}}{2}}}
sin
(
π
/
6
)
=
sin
(
30
∘
)
=
cos
(
π
/
3
)
=
cos
(
60
∘
)
=
1
2
{\displaystyle \sin \left(\pi /6\right)=\sin \left(30^{\circ }\right)=\cos \left(\pi /3\right)=\cos \left(60^{\circ }\right)={1 \over 2}\,}
cos
(
π
/
6
)
=
cos
(
30
∘
)
=
sin
(
π
/
3
)
=
sin
(
60
∘
)
=
3
2
{\displaystyle \cos \left(\pi /6\right)=\cos \left(30^{\circ }\right)=\sin \left(\pi /3\right)=\sin \left(60^{\circ }\right)={{\sqrt {3}} \over 2}\,}
tan
(
π
/
6
)
=
tan
(
30
∘
)
=
cot
(
π
/
3
)
=
cot
(
60
∘
)
=
1
3
{\displaystyle \tan \left(\pi /6\right)=\tan \left(30^{\circ }\right)=\cot \left(\pi /3\right)=\cot \left(60^{\circ }\right)={1 \over {\sqrt {3}}}\,}
ចំពោះសេចក្តីលំអិត សូមមើលចំនួនថេរត្រីកោណមាត្រពិត ។
តំលៃពិសេសនៃអនុគមន៍ត្រីកោណមាត្រ ខាងក្រោមនេះជាតារាងតំលៃពិសេសនៃអនុគមន៍ត្រីកោណមាត្រដែលត្រូវបានគេប្រើប្រាស់ជាទូទៅ។
ឈ្មោះអនុគមន៍
0
(
0
∘
)
{\displaystyle 0\ (0^{\circ })}
π
12
(
15
∘
)
{\displaystyle {\frac {\pi }{12}}\ (15^{\circ })}
π
6
(
30
∘
)
{\displaystyle {\frac {\pi }{6}}\ (30^{\circ })}
π
4
(
45
∘
)
{\displaystyle {\frac {\pi }{4}}\ (45^{\circ })}
π
3
(
60
∘
)
{\displaystyle {\frac {\pi }{3}}\ (60^{\circ })}
5
π
12
(
75
∘
)
{\displaystyle {\frac {5\pi }{12}}\ (75^{\circ })}
π
2
(
90
∘
)
{\displaystyle {\frac {\pi }{2}}\ (90^{\circ })}
sin
0
{\displaystyle 0}
6
−
2
4
{\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
6
+
2
4
{\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}
1
{\displaystyle 1}
cos
1
{\displaystyle 1}
6
+
2
4
{\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
6
−
2
4
{\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}
0
{\displaystyle 0}
tan
0
{\displaystyle 0}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
2
+
3
{\displaystyle 2+{\sqrt {3}}}
∞
{\displaystyle \infty }
cot
∞
{\displaystyle \infty }
2
+
3
{\displaystyle 2+{\sqrt {3}}}
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
2
−
3
{\displaystyle 2-{\sqrt {3}}}
0
{\displaystyle 0}
sec
1
{\displaystyle 1}
6
−
2
{\displaystyle {\sqrt {6}}-{\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
6
+
2
{\displaystyle {\sqrt {6}}+{\sqrt {2}}}
∞
{\displaystyle \infty }
csc
∞
{\displaystyle \infty }
6
+
2
{\displaystyle {\sqrt {6}}+{\sqrt {2}}}
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
6
−
2
{\displaystyle {\sqrt {6}}-{\sqrt {2}}}
1
{\displaystyle 1}
អនុគមន៍ត្រីកោណមាត្រជាអនុគមន៍ខួប និងមិនមែនជាអនុគមន៍មួយទល់នឹងមួយ និង មិនមែនជាអនុគមន៍ប្រកាន់ ទេ។ ក្នុងចន្លោះពិតលើដែនកំនត់ជាក់លាក់ណាមួយ អនុគមន៍ត្រីកោណមាត្រជាអនុគមន៍ប្រកាន់ ។ អនុគមន៍ច្រាស់របស់វា (arcsin, arccos, arctan, arccosec, arccotg និង arcsec) ជាទូទៅកំនត់ដោយ៖
ចំពោះគ្រប់ចំនួនពិត x និង y
−
1
≤
x
≤
1
,
−
π
2
≤
y
≤
π
2
{\displaystyle \ -1\leq x\leq 1,\quad -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}
y
=
A
r
c
s
i
n
(
x
)
{\displaystyle \ y=Arcsin(x)}
x
=
sin
(
y
)
{\displaystyle \ x=\sin(y)}
ចំពោះគ្រប់ចំនួនពិត x និង y
−
1
≤
x
≤
1
,
0
≤
y
≤
π
{\displaystyle -1\leq x\leq 1,\quad 0\leq y\leq \pi }
y
=
A
r
c
c
o
s
(
x
)
{\displaystyle \ y=Arccos(x)}
x
=
cos
(
y
)
{\displaystyle \ x=\cos(y)}
ចំពោះគ្រប់ចំនួនពិត x និង y
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}
y
=
A
r
c
t
a
n
(
x
)
{\displaystyle \ y=Arctan(x)}
x
=
tan
(
y
)
{\displaystyle \ x=\tan(y)}
ចំពោះគ្រប់ចំនួនពិត x និង y
(
x
≤
−
1
{\displaystyle \ (x\leq -1}
x
≥
1
)
,
(
−
π
2
≤
y
≤
π
2
{\displaystyle \ x\geq 1),\quad (-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}
y
≠
0
{\displaystyle \ y\neq 0}
y
=
a
r
c
c
o
s
e
c
(
x
)
{\displaystyle \ y=arccosec(x)}
x
=
c
o
s
e
c
(
y
)
{\displaystyle \ x=cosec(y)}
ចំពោះគ្រប់ចំនួនពិត x និង y
(
x
≤
−
1
{\displaystyle \ (x\leq -1}
x
≥
1
)
,
(
0
≤
y
≤
π
{\displaystyle \ x\geq 1),\quad (0\leq y\leq \pi }
y
≠
π
2
)
{\displaystyle \ y\neq {\frac {\pi }{2}})}
y
=
a
r
c
s
e
c
(
x
)
{\displaystyle \ y=arcsec(x)}
x
=
sec
(
y
)
{\displaystyle \ x=\sec(y)}
ចំពោះគ្រប់ចំនួនពិត x និង y
x
?
0
,
(
0
<
y
<
π
{\displaystyle \ x?0,\quad (0<y<\pi }
y
?
π
2
)
{\displaystyle \ y?{\frac {\pi }{2}})}
y
=
a
r
c
c
o
t
g
(
x
)
{\displaystyle \ y=arccotg(x)}
x
=
c
o
t
g
(
y
)
{\displaystyle \ x=cotg(y)}
អនុគមន៍ ទាំងនេះអាចសរសេរក្រោមទំរង់អាំងតេក្រាលមិនកំនត់ ៖
Arcsin
(
x
)
=
∫
1
1
−
x
2
d
x
{\displaystyle \operatorname {Arcsin} (x)=\int {\frac {1}{\sqrt {1-x^{2}}}}dx}
Arccos
(
x
)
=
∫
−
1
1
−
x
2
d
x
{\displaystyle \operatorname {Arccos} (x)=\int -{\frac {1}{\sqrt {1-x^{2}}}}dx}
Arctan
(
x
)
=
∫
1
1
+
x
2
d
x
{\displaystyle \operatorname {Arctan} (x)=\int {\frac {1}{1+x^{2}}}dx}
a
r
c
c
o
s
e
c
(
x
)
=
∫
−
1
x
x
2
−
1
d
x
{\displaystyle \mathrm {arccosec} (x)=\int -{\frac {1}{x{\sqrt {x^{2}-1}}}}dx}
arcsec
(
x
)
=
∫
1
x
x
2
−
1
d
x
{\displaystyle \operatorname {arcsec}(x)=\int {\frac {1}{x{\sqrt {x^{2}-1}}}}dx}
a
r
c
c
o
t
g
(
x
)
=
∫
−
1
1
+
x
2
d
x
{\displaystyle \mathrm {arccotg} (x)=\int -{\frac {1}{1+x^{2}}}dx}
សមភាពអនុវត្ត:
cos
(
Arcsin
(
x
)
)
=
1
−
x
2
{\displaystyle \cos(\operatorname {Arcsin} (x))={\sqrt {1-x^{2}}}}
sin
(
Arccos
(
x
)
)
=
1
−
x
2
{\displaystyle \sin(\operatorname {Arccos} (x))={\sqrt {1-x^{2}}}}
sin
(
Arctan
(
x
)
)
=
x
1
+
x
2
{\displaystyle \sin(\operatorname {Arctan} (x))={\frac {x}{\sqrt {1+x^{2}}}}}
tan
(
Arcsin
(
x
)
)
=
x
1
−
x
2
{\displaystyle \tan(\operatorname {Arcsin} (x))={\frac {x}{\sqrt {1-x^{2}}}}}
tan
(
Arccos
(
x
)
)
=
1
−
x
2
x
{\displaystyle \tan(\operatorname {Arccos} (x))={\frac {\sqrt {1-x^{2}}}{x}}}
cos
(
Arctan
(
x
)
)
=
1
1
+
x
2
{\displaystyle \cos(\operatorname {Arctan} (x))={\frac {1}{\sqrt {1+x^{2}}}}}
អនុគមន៍ត្រីកោណមាត្រគឺជាអនុគមន៍ដ៏មានសារសំខាន់នៅក្នុងត្រីកោណមាត្រ ។
ទ្រឹស្តីបទស៊ីនុស ត្រីកោណ មួយដែលមានរង្វាស់ជ្រុង a, b និង c និងមុំ A, B និង C ជាមុំឈមនឹងជ្រុងទាំងនេះរៀងគ្នា គេបាន៖
sin
A
a
=
sin
B
b
=
sin
C
c
{\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}\,}
ឬសមមូលនឹង
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R\,}
ដែល R ជាកាំ នៃរង្វង់ចារឹកក្រៅ ត្រីកោណ ABC ។
ទ្រឹស្តីបទកូស៊ីនុសគឺជាបន្លាយនៃទ្រឹស្តីបទពីតាករ (មានន័យថាជាករណីទូទៅនៃទ្រឹស្តីបទពីតាករ)៖
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C\,}
ឬ
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,}
ក្នុងរូបមន្តនេះមុំត្រង់កំពូល C គឺជាមុំឈមនឹងជ្រុងមានរង្វាស់ c ។ ទ្រឹស្តីបទនេះអាចបង្ហាញដោយចែកត្រីកោណជាពីរបំនែកត្រីកោណកែង រួចប្រើទ្រឹស្តីបទពីតាករ ។ ទ្រឹស្តីបទកូស៊ីនុសត្រូវបានគេប្រើប្រាស់ជាញឹកញាប់ក្នុងការកំនត់ប្រវែងជ្រុងមួយនៃត្រីកោណនៅពេលគេស្គាល់ជ្រុងឈម និង មុំមួយ។ គេអាចប្រើវាដើម្បីរកកូស៊ីនុសនៃមុំមួយនៅពេលដែលគេស្គាល់ប្រវែងជ្រុងទាំងអស់នៃត្រីកោណ។
a
+
b
a
−
b
=
tan
[
1
2
(
A
+
B
)
]
tan
[
1
2
(
A
−
B
)
]
{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}\,}
បំរើបំរាស់នៃអនុគមន៍ត្រីកោណមាត្រមិនកំនត់តែនៅក្នុងត្រីកោណ ទេ។ អនុគមន៍ត្រីកោណមាត្រជាអនុគមន៍ខួប ដែលក្រាបរបស់វាត្រូវនឹងម៉ូដែលរលកដែលត្រូវបានគេប្រើប្រាស់ក្នុងបាតុភូតម៉ូដែលដូចជាលំយោលនៃសំលែង ឬ រលកពន្លឺ។ សញ្ញានិមួយៗអាចត្រូវបានគេសរសេរជាផលបូក (ជាធម្មតាអនន្ត) អនុគមន៍ស៊ីនុស ឬ កូស៊ីនុសនៃដេរីវេប្រេកង់ ដែលវាជាស៊េរីហ្វួរា (Fourier series)។
ចំពោះរូបមន្តនៃទំនាក់ទំនងរវាងអនុគមន៍ត្រីកោណមាត្រ សូមមើលតារាងរូបមន្តត្រីកោណមាត្រ ។
[ កែប្រែ ] ក្រៅពីអនុគមន៍ត្រីកោណមាត្រគ្រឹះចំនួន នៅមានអនុគមន៍ត្រីកោណមាត្រចំនួន៦ផ្សេងទៀត៖
វែរស៊ីនុស
versin
(
θ
)
=
1
−
cos
(
θ
)
=
2
sin
2
(
θ
2
)
{\displaystyle {\textrm {versin}}(\theta )=1-\cos(\theta )=2\sin ^{2}\left({\frac {\theta }{2}}\right)\,}
កូវែរស៊ីនុស
coversin
(
θ
)
=
versin
(
π
/
2
−
θ
)
=
1
−
sin
(
θ
)
{\displaystyle {\textrm {coversin}}(\theta )={\textrm {versin}}(\pi /2-\theta )=1-\sin(\theta )\,}
កន្លះវែរស៊ីនុស
haversin
(
θ
)
=
versin
(
θ
)
2
=
sin
2
(
θ
2
)
{\displaystyle {\textrm {haversin}}(\theta )={\frac {{\textrm {versin}}(\theta )}{2}}=\sin ^{2}\left({\frac {\theta }{2}}\right)}
កន្លះកូវែរស៊ីនុស
hacoversin
(
θ
)
=
haversin
(
π
2
−
θ
)
=
coversin
(
θ
)
2
{\displaystyle {\textrm {hacoversin}}(\theta )={\textrm {haversin}}\left({\frac {\pi }{2}}-\theta \right)={\frac {{\textrm {coversin}}(\theta )}{2}}}
អិចសេកង់
exsec
(
θ
)
=
sec
(
θ
)
−
1
{\displaystyle {\textrm {exsec}}(\theta )=\sec(\theta )-1\,}
អិចកូសេកង់
excsc
(
θ
)
=
exsec
(
π
/
2
−
θ
)
=
csc
(
θ
)
−
1
{\displaystyle {\textrm {excsc}}(\theta )={\textrm {exsec}}(\pi /2-\theta )=\csc(\theta )-1\!}
















































































































































































































































![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(A+B)]}{\tan[{\frac {1}{2}}(A-B)]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0113d7104c458114da7266df93effcff9b458f)






