ទ្រឹស្តីបទមេដ្យាន គឺជាទ្រឹស្តីបទសិក្សាពីទំនាក់ទំនងរវាងរង្វាស់មេដ្យាន នៃត្រីកោណ និងរង្វាស់ជ្រុងនិមួយៗរបស់វា។ ទ្រឹស្តីបទមេដ្យានជាករណីពិសេសរបស់ទ្រឹស្តីបទអាប៉ូឡូនុស (Apollonius' theorem) ។
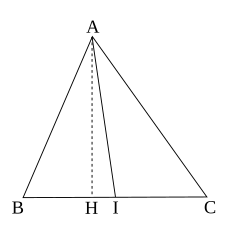
គេមានត្រីកោណ ABC ដែល AI ជារង្វាស់មេដ្យាន គូសចេញពីកំពូល A ។ គេបានទំនាក់ដូចខាងក្រោម:
A
B
2
+
A
C
2
=
2
B
I
2
+
2
A
I
2
{\displaystyle AB^{2}+AC^{2}=2BI^{2}+2AI^{2}\,}
A
B
2
+
A
C
2
=
1
2
B
C
2
+
2
A
I
2
{\displaystyle AB^{2}+AC^{2}={1 \over 2}BC^{2}+2AI^{2}\,}
លក្ខណៈនេះជាករណីធម្មតាដោយការកាត់បន្ថយនៃអនុគមន៍ស្តាលែរលេបនីស្ស (scalar function of Leibniz):
A
B
2
+
A
C
2
=
(
A
I
→
+
I
B
→
)
2
+
(
A
I
→
+
I
C
→
)
2
{\displaystyle AB^{2}+AC^{2}=({\overrightarrow {AI}}+{\overrightarrow {IB}})^{2}+({\overrightarrow {AI}}+{\overrightarrow {IC}})^{2}}
គេពន្លាត:
A
B
2
+
A
C
2
=
A
I
2
+
I
B
2
+
2
A
I
→
.
I
B
→
+
A
I
2
+
I
C
2
+
2
A
I
→
.
I
C
→
{\displaystyle AB^{2}+AC^{2}=AI^{2}+IB^{2}+2{\overrightarrow {AI}}.{\overrightarrow {IB}}+AI^{2}+IC^{2}+2{\overrightarrow {AI}}.{\overrightarrow {IC}}}
ចំនុច I ជាចំនុចកណ្តាល [BC] ដូចនេះ
I
B
→
{\displaystyle {\overrightarrow {IB}}}
I
C
→
{\displaystyle {\overrightarrow {IC}}}
I
C
2
=
I
B
2
{\displaystyle IC^{2}=IB^{2}}
A
B
2
+
A
C
2
=
2
A
I
2
+
2
I
B
2
{\displaystyle AB^{2}+AC^{2}=2AI^{2}+2IB^{2}\,}
តាង H ជាចំណោលនៃកំពស់ត្រីកោណ ពីកំពូល A មកលើជ្រុង BC ចែកត្រីកោណ ABC ជាពីរត្រីកោណកែង BHA និង AHC ។ ដោយអនុវត្តទ្រឹស្តីបទពីតាករ គេបាន
A
B
2
=
B
H
2
+
A
H
2
{\displaystyle AB^{2}=BH^{2}+AH^{2}\,}
A
C
2
=
A
H
2
+
H
C
2
{\displaystyle AC^{2}=AH^{2}+HC^{2}\,}
A
I
2
=
I
H
2
+
A
H
2
{\displaystyle AI^{2}=IH^{2}+AH^{2}\,}
ហេតុនេះ
A
B
2
+
A
C
2
=
B
H
2
+
2
A
H
2
+
H
C
2
{\displaystyle AB^{2}+AC^{2}=BH^{2}+2AH^{2}+HC^{2}\,}
ដោយសំដែង BH និង HC ជាអនុគមន៍នៃ BI និង IH (ដែល I ជាចំនុចគណ្តាលនៃ BC និង BI=IC) ។ កត់សំគាល់ផងដែរចំពោះករណីពិសេស ជើង H នៃកំពស់គូសចេញពីកំពូល A មកលើអង្កត់ [BI] នៅចន្លោះ B និង I ប៉ុន្តែវាផ្ទៀងផ្ទាត់គ្រប់ករណី
B
H
=
B
I
−
I
H
{\displaystyle BH=BI-IH\,}
H
C
=
I
C
+
I
H
=
B
I
+
I
H
{\displaystyle HC=IC+IH=BI+IH\,}
ជំនួសចូលក្នុងកន្សោមខាងលើ គេបាន
A
B
2
+
A
C
2
=
(
B
I
−
I
H
)
2
+
2
A
H
2
+
(
B
I
+
I
H
)
2
{\displaystyle AB^{2}+AC^{2}=(BI-IH)^{2}+2AH^{2}+(BI+IH)^{2}\,}
A
B
2
+
A
C
2
=
B
I
2
−
2
B
I
.
I
H
+
I
H
2
+
2
A
H
2
+
B
I
2
+
2
B
I
.
I
H
+
I
H
2
{\displaystyle AB^{2}+AC^{2}=BI^{2}-2BI.IH+IH^{2}+2AH^{2}+BI^{2}+2BI.IH+IH^{2}\,}
A
B
2
+
A
C
2
=
2
B
I
2
+
2
I
H
2
+
2
A
H
2
=
2
B
I
2
+
2
(
I
H
2
+
A
H
2
)
{\displaystyle AB^{2}+AC^{2}=2BI^{2}+2IH^{2}+2AH^{2}=2BI^{2}+2(IH^{2}+AH^{2})\,}
ឬគេអាចថា
I
H
2
+
A
H
2
=
A
I
2
{\displaystyle IH^{2}+AH^{2}=AI^{2}\,}
ដោយជំនួសវាចូលក្នុងសមីការខាងលើគេបាន
A
B
2
+
A
C
2
=
2
B
I
2
+
2
A
I
2
{\displaystyle AB^{2}+AC^{2}=2BI^{2}+2AI^{2}\,}
[ កែប្រែ ] ជាមួយនឹងផលគុណស្កាលែរ:
A
B
2
−
A
C
2
=
2
B
C
→
.
I
H
→
{\displaystyle AB^{2}-AC^{2}=2{\overrightarrow {BC}}.{\overrightarrow {IH}}}
|
A
B
2
−
A
C
2
|
=
2
B
C
×
I
H
{\displaystyle \left|AB^{2}-AC^{2}\right|=2BC\times IH}
តាមពិត :
A
B
2
−
A
C
2
=
(
A
B
→
+
A
C
→
)
.
(
A
B
→
−
A
C
→
)
=
2
A
I
→
.
(
A
B
→
+
C
A
→
)
=
2
A
I
→
.
C
B
→
{\displaystyle AB^{2}-AC^{2}=({\overrightarrow {AB}}+{\overrightarrow {AC}}).({\overrightarrow {AB}}-{\overrightarrow {AC}})=2{\overrightarrow {AI}}.({\overrightarrow {AB}}+{\overrightarrow {CA}})=2{\overrightarrow {AI}}.{\overrightarrow {CB}}}
ចំណោលនៃ
A
I
→
{\displaystyle {\overrightarrow {AI}}}
B
C
→
{\displaystyle {\overrightarrow {BC}}}
H
I
→
{\displaystyle {\overrightarrow {HI}}}
A
I
→
C
B
→
=
H
I
→
.
C
B
→
=
B
C
→
.
I
H
→
{\displaystyle {\overrightarrow {AI}}{\overrightarrow {CB}}={\overrightarrow {HI}}.{\overrightarrow {CB}}={\overrightarrow {BC}}.{\overrightarrow {IH}}}
ផលគុណស្កាលែរនៃពីរវ៉ិចទ័រស្របគ្នាគឺស្មើនឹង
B
C
×
I
H
{\displaystyle BC\times IH}
[ កែប្រែ ] បើ I ជាចំនុចកណ្តាល [BC] គេបាន :
A
B
→
+
A
C
→
=
2
A
I
→
{\displaystyle {\overrightarrow {AB}}+{\overrightarrow {AC}}=2{\overrightarrow {AI}}}
[ កែប្រែ ] គេមានត្រីកោណ MBC ។ គេគូសបន្ទាត់មួយចេញពី M កាត់ជ្រុង [BC] ត្រង់ I ។ តាង
k
=
I
C
I
B
{\displaystyle k={\frac {IC}{IB}}}
M
I
2
=
k
M
B
2
+
M
C
2
1
+
k
−
(
I
B
.
I
C
)
{\displaystyle MI^{2}={\frac {kMB^{2}+MC^{2}}{1+k}}-(IB.IC)}