រូបមន្តដឺម័រ (De Moivre's formula) ត្រូវបានគេហៅដោយយកតាមឈ្មោះរបស់លោក អាប្រាហាម ដឺ ម័រ (Abraham de Moivre) ដែលជាជនជាតិបារាំង ដោយបានចែងថាចំពោះគ្រប់ចំនួនកុំផ្លិច (និងជាពិសេសចំពោះគ្រប់ចំនួនពិត) x និង គ្រប់ចំនួនគត់ n គេបាន
(
cos
x
+
i
sin
x
)
n
=
cos
(
n
x
)
+
i
sin
(
n
x
)
{\displaystyle \color {blue}\left(\cos x+i\sin x\right)^{n}=\cos \left(nx\right)+i\sin \left(nx\right)\,}
រូបមន្តនេះមានសារៈសំខាន់ពីព្រោះវាភ្ជាប់ចំនួនកុំផ្លិច (i តំណាងអោយឯកតានិម្មិត) និង ត្រីកោណមាត្រ ។ កន្សោម
cos
x
+
i
sin
x
{\displaystyle \cos x+i\sin x\,}
c
i
s
x
{\displaystyle cisx\,}
រូមមន្តដឺម័រអាចត្រូវបានទាញចេញដោយងាយដោយប្រើរូបមន្តអយល័រ
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x\,}
និងតាមទ្រឹស្តីបទអិចស្ប៉ូណង់ស្យែល
(
e
i
x
)
n
=
e
i
n
x
{\displaystyle \left(e^{ix}\right)^{n}=e^{inx}\,}
តាមរូបមន្តអយល័រ គេបាន
e
i
(
n
x
)
=
cos
(
n
x
)
+
i
sin
(
n
x
)
{\displaystyle e^{i(nx)}=\cos(nx)+i\sin(nx)\,}
គេមាន
x
∈
R
{\displaystyle x\in \mathbb {R} }
យើងសិក្សា៣ករណី
(១). ករណី
n
>
0
{\displaystyle n>0\,}
n
=
1
{\displaystyle n=1\,}
k
{\displaystyle k\,}
(
cos
x
+
i
sin
x
)
k
=
cos
(
k
x
)
+
i
sin
(
k
x
)
{\displaystyle \left(\cos x+i\sin x\right)^{k}=\cos \left(kx\right)+i\sin \left(kx\right)\,}
យើងបាន
ចំពោះ
n
=
1
;
⇒
(
cos
x
+
i
sin
x
)
1
=
cos
(
1
⋅
x
)
+
i
sin
(
1
⋅
x
)
{\displaystyle n=1;\quad \Rightarrow (\cos x+i\sin x)^{1}=\cos(1\cdot x)+i\sin(1\cdot x)\qquad \,}
ពិត
ចំពោះ
n
=
2
;
{\displaystyle n=2\,;}
⇒
(
cos
x
+
i
sin
x
)
2
=
cos
2
x
−
sin
2
x
+
2
i
cos
x
sin
x
=
cos
(
2
⋅
x
)
+
i
sin
(
2
⋅
x
)
{\displaystyle {\begin{aligned}\Rightarrow (\cos x+i\sin x)^{2}&=\cos ^{2}x-\sin ^{2}x+2i\cos x\sin x\\&=\cos(2\cdot x)+i\sin(2\cdot x)\qquad \\\end{aligned}}}
ឧបមាថាវាពិតដល់
n
=
k
+
1
{\displaystyle n=k+1\;}
(
cos
x
+
i
sin
x
)
k
+
1
=
(
cos
x
+
i
sin
x
)
k
(
cos
x
+
i
sin
x
)
=
[
cos
(
k
x
)
+
i
sin
(
k
x
)
]
(
cos
x
+
i
sin
x
)
=
cos
(
k
x
)
cos
x
−
sin
(
k
x
)
sin
x
+
i
[
cos
(
k
x
)
sin
x
+
sin
(
k
x
)
cos
x
]
=
cos
[
(
k
+
1
)
x
]
+
i
sin
[
(
k
+
1
)
x
]
{\displaystyle {\begin{alignedat}{2}\left(\cos x+i\sin x\right)^{k+1}&=\left(\cos x+i\sin x\right)^{k}\left(\cos x+i\sin x\right)\\&=\left[\cos \left(kx\right)+i\sin \left(kx\right)\right]\left(\cos x+i\sin x\right)&&\qquad \\&=\cos \left(kx\right)\cos x-\sin \left(kx\right)\sin x+i\left[\cos \left(kx\right)\sin x+\sin \left(kx\right)\cos x\right]\\&=\cos \left[\left(k+1\right)x\right]+i\sin \left[\left(k+1\right)x\right]&&\qquad \end{alignedat}}}
យើងសន្និដ្ឋានថាលទ្ធផលពិតចំពោះ
n
=
k
+
1
{\displaystyle n=k+1\,}
n
=
k
{\displaystyle n=k\,}
n
≥
1
{\displaystyle n\geq 1\,}
(២) . ករណី
n
=
0
{\displaystyle n=0\,}
cos
(
0
x
)
+
i
sin
(
0
x
)
=
1
+
i
0
=
1
{\displaystyle \cos(0x)+i\sin(0x)=1+i0=1\,}
z
0
=
1
{\displaystyle z^{0}=1}
(៣) . ករណី
n
<
0
{\displaystyle n<0\,}
m
{\displaystyle m\,}
n
=
−
m
{\displaystyle n=-m\,}
(
cos
x
+
i
sin
x
)
n
=
(
cos
x
+
i
sin
x
)
−
m
=
1
(
cos
x
+
i
sin
x
)
m
=
1
(
cos
m
x
+
i
sin
m
x
)
=
cos
(
m
x
)
−
i
sin
(
m
x
)
=
cos
(
−
m
x
)
+
i
sin
(
−
m
x
)
=
cos
(
n
x
)
+
i
sin
(
n
x
)
{\displaystyle {\begin{aligned}\left(\cos x+i\sin x\right)^{n}&=\left(\cos x+i\sin x\right)^{-m}\\&={\frac {1}{\left(\cos x+i\sin x\right)^{m}}}\\&={\frac {1}{\left(\cos mx+i\sin mx\right)}}\\&=\cos \left(mx\right)-i\sin \left(mx\right)\\&=\cos \left(-mx\right)+i\sin \left(-mx\right)\\&=\cos \left(nx\right)+i\sin \left(nx\right)\end{aligned}}}
ដូចនេះរូបមន្តពិតចំពោះគ្រប់តំលៃជាចំនួនគត់នៃ n ។
ប្រសិនបើ z និង w' គឺជាចំនួនកុំផ្លិច នោះគេបាន
(
cos
z
+
i
sin
z
)
w
{\displaystyle \left(\cos z+i\sin z\right)^{w}}
គឺជាអនុគមន៍មានតំលៃច្រើន ដែល
cos
(
w
z
)
+
i
sin
(
w
z
)
{\displaystyle \cos(wz)+i\sin(wz)\,}
មិនមែន។ ដូចនេះគេអាចពោលថា
cos
(
w
z
)
+
i
sin
(
w
z
)
{\displaystyle \cos(wz)+i\sin(wz)\,}
គឺជាតំលៃមួយនៃ
(
cos
z
+
i
sin
z
)
w
{\displaystyle \left(\cos z+i\sin z\right)^{w}\,}
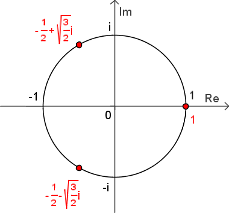
គំនូសមនៅលើ ប្លង់កុំផ្លិច នៃរឹសគូបនៃ១ រូបមន្តនេះអាចត្រូវបានគេប្រើប្រាស់ដើម្បីរករឹសទី n នៃចំនួនកុំផ្លិច ។ ប្រសិនបើ z ជាចំនួនកុំផ្លិច សរសេរក្នុងទំរង់ប៉ូលែរជា
z
=
r
(
cos
x
+
i
sin
x
)
{\displaystyle z=r\left(\cos x+i\sin x\right)\,}
គេបាន
z
1
n
=
[
r
(
cos
x
+
i
sin
x
)
]
1
n
=
r
1
n
[
cos
(
x
+
2
k
π
n
)
+
i
sin
(
x
+
2
k
π
n
)
]
{\displaystyle z^{{}^{\frac {1}{n}}}=\left[r\left(\cos x+i\sin x\right)\right]^{{}^{\frac {1}{n}}}=r^{{}^{\frac {1}{n}}}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]}
ដែល k ជាចំនួនគត់ ។ ដើម្បីទទួល n រឹសផ្សេងៗគ្នានៃ z ចាំបាច់ត្រូវការអោយតំលៃនៃ k ពី 0 ដល់ n-1 ។
















![{\displaystyle {\begin{alignedat}{2}\left(\cos x+i\sin x\right)^{k+1}&=\left(\cos x+i\sin x\right)^{k}\left(\cos x+i\sin x\right)\\&=\left[\cos \left(kx\right)+i\sin \left(kx\right)\right]\left(\cos x+i\sin x\right)&&\qquad \\&=\cos \left(kx\right)\cos x-\sin \left(kx\right)\sin x+i\left[\cos \left(kx\right)\sin x+\sin \left(kx\right)\cos x\right]\\&=\cos \left[\left(k+1\right)x\right]+i\sin \left[\left(k+1\right)x\right]&&\qquad \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560dc0b7120bac64196176ef8ad703526566563c)














![{\displaystyle z^{{}^{\frac {1}{n}}}=\left[r\left(\cos x+i\sin x\right)\right]^{{}^{\frac {1}{n}}}=r^{{}^{\frac {1}{n}}}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eab1404986f106fd12c1a60f82f0222cd55f9c5)