ទ្រឹស្តីបទតង់សង់

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

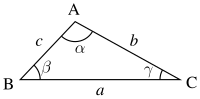
រូបត្រីកោណABC

ក្នុងត្រីកោណមាត្រ ទ្រឹស្តីបទតង់សង់ (ឬហៅថាច្បាប់តង់សង់)ជាទ្រឹស្តីសិក្សាអំពីទំនាក់ទំនងរវាងជ្រុងទាំង៣នៃត្រីកោណ និងតង់សង់នៃមុំ។

រូបខាងស្តាំជាត្រីកោណដែលមានជ្រុងប្រវែង a b និង c មុំឈមនៃជ្រុងនិមួយៗ α β និង γ នោះគេបានទ្រឹស្តីបទតង់សង់សំដែងដោយ

$\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}$

ដែល

$a = BC \,$ និង $\alpha = \ang A \,$
$b = AC \,$ និង $\beta = \ang B \,$
$c = AB \,$ និង $\gamma = \ang C \,$

ទ្រឹស្តីបទនេះត្រូវបានគេប្រើនៅពេលគេស្គាល់ប្រវែងជ្រុងពីរនិងមុំមួយ ឬប្រវែងជ្រុងមួយនិងមុំពីរ។

ដូចគ្នាដែរចំពោះទំនាក់ទំនងផលធៀបនៃជ្រុងផ្សេងៗទៀត៖

$\frac{b-c}{b+c}=\frac{\mathrm{tan}\, \frac{\beta -\gamma }{2}}{\mathrm{tan}\, \frac{\beta +\gamma }{2}}$
$\frac{c-a}{c+a}=\frac{\mathrm{tan}\, \frac{\gamma -\alpha }{2}}{\mathrm{tan}\, \frac{\gamma +\alpha }{2}}$

[កែប្រែ] សំរាយបញ្ជាក់

សំរាយបញ្ជាក់៖ $\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}$

ដើម្បីស្រាយបញ្ជាក់ទ្រឹស្តីបទនេះ យើងត្រូវប្រើទ្រឹស្តីបទស៊ីនុស

$\frac{a}{\sin{\alpha}} = \frac{b}{\sin{\beta}}$

យើងអាចនិយាយថាមាន q ដែល

$q = \frac{a}{\sin{\alpha}} = \frac{b}{\sin{\beta}}$

តាមរយៈទំនាក់ទំនងនេះយើងអាចកំនត់តំលៃនៃ b និងa ដែល

$a = q \sin{\alpha} \,$
$b = q \sin{\beta} \,$

ដោយជំនួសតំលៃនៃ a និងb ទៅក្នុងសមីការដើម គេបាន

$\frac{a-b}{a+b} = \frac{q \sin \alpha -q\sin\beta}{q\sin\alpha+q\sin\beta} = \frac{ \sin \alpha -\sin\beta}{\sin\alpha+\sin\beta}$

បំបាត់ q និងប្រើលក្ខណៈនៃត្រីកោណមាត្រយើងបាន

$\sin(\alpha) + \sin(\beta) = 2 \sin\left( \frac{\alpha + \beta}{2} \right) \cos\left( \frac{\alpha - \beta}{2} \right) \;$

ចំពោះ $\scriptstyle{x\,=\,\alpha}$ និង $\scriptstyle{y\,=\,\pm\beta}$ ដូច្នេះយើងបាន

$\frac{a-b}{a+b} = \frac{ 2 \sin\left( \frac{\alpha -\beta}{2} \right) \cos\left( \frac{\alpha+\beta}{2}\right) }{ 2 \sin\left( \frac{\alpha +\beta}{2} \right) \cos\left( \frac{\alpha-\beta}{2}\right)} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}$

(លក្ខណៈផ្សេងទៀត $\tan\left( \frac{\alpha \pm \beta}{2} \right) = \frac{\sin\alpha \pm \sin\beta}{\cos\alpha + \cos\beta}$ )

[កែប្រែ] សូមមើលផងដែរ

ទ្រឹស្តីបទតង់សង់

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

[កែប្រែ] សំរាយបញ្ជាក់

[កែប្រែ] សូមមើលផងដែរ

ការមើល

ឧបករណ៍ផ្ទាល់ខ្លួន

ស្វែងរក

ទិសដៅ

សហគមន៍

ប្រអប់ឧបករណ៍

ជាភាសាដទៃទៀត

ទ្រឹស្តីបទ​តង់សង់

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

[កែប្រែ] សំរាយបញ្ជាក់

[កែប្រែ] សូមមើលផងដែរ

ការមើល

ឧបករណ៍ផ្ទាល់ខ្លួន

ស្វែងរក

ទិសដៅ

សហគមន៍

ប្រអប់​ឧបករណ៍

ជាភាសាដទៃទៀត

ទ្រឹស្តីបទតង់សង់

ប្រអប់ឧបករណ៍