នៅក្នុងត្រីកោណមាត្រ ទ្រឹស្តីបទស៊ីនុស (ឬច្បាប់ស៊ីនុស ឬរូបមន្តស៊ីនុស) ជាទ្រឹស្តីបទសិក្សាអំពីត្រីកោណ នៅក្នុងប្លង់ ។
ត្រីកោណ ABC ដែលមានជ្រុង a, b, c, ក្រលាផ្ទៃ S រង្វង់ចារឹកក្រៅកាំ R និងមុំ A, B, Cគេមានត្រីកោណ ABC ដែលមានជ្រុង a, b និង c និង A, B និង C ជាមុំឈមនៃជ្រុងទាំងនេះ(∠A=A , ∠B=B , ∠C=C ) និង
R
{\displaystyle R\,}
រង្វង់ ចារឹកក្រៅត្រីកោណ ABC នោះគេបានទ្រឹស្តីបទស៊ីនុសបង្ហាញដូចខាងក្រោម
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle \color {blue}{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R}
ទ្រឹស្តីបទនេះត្រូវបានគេប្រើប្រាស់ដើម្បីគណនាជ្រុងនៃត្រីកោណ ដែលនៅសល់ ប្រសិនបើគេស្គាល់តំលៃនៃមុំ ២ និងជ្រុងមួយ។ វាក៏អាចត្រូវបានគេប្រើបានដែល នៅគេស្គាល់ជ្រុងពីរ និងមុំមួយ។
2
R
=
a
b
c
2
S
=
a
b
c
2
p
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
=
2
a
b
c
(
a
2
+
b
2
+
c
2
)
2
−
2
(
a
4
+
b
4
+
c
4
)
{\displaystyle {\begin{aligned}2R={\frac {abc}{2S}}&{}={\frac {abc}{2{\sqrt {p(p-a)(p-b)(p-c)}}}}\\&{}={\frac {2abc}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}\end{aligned}}}
ដែល
S
{\displaystyle S\,}
ក្រលាផ្ទៃនៃត្រីកោណ និង
p
{\displaystyle p\,}
កន្លះបរិមាត្រ ។
p
=
a
+
b
+
c
2
{\displaystyle p={\frac {a+b+c}{2}}}
△ABC កំពស់ h គូសចេញពីកំពូល C សំរាយបញ្ជាក់
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle \color {blue}{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}}
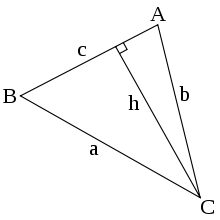
គេមានត្រីកោណ ABC ដែលមានរង្វាស់ជ្រុងរៀងគ្នា a, b, c និងមុំ A B C បង្ហាញដូចរូបខាងស្តាំ។ h ជាកំពស់ គូសចេញពីកំពូល C មកជ្រុង AB ។ តាមនិយមន័យវាចែកត្រីកោណ ABC ជាពីរត្រីកោណកែង ។ គេបាន
sin
A
=
h
b
{\displaystyle \sin A={\frac {h}{b}}}
sin
B
=
h
a
{\displaystyle \sin B={\frac {h}{a}}}
⇒
h
=
b
(
sin
A
)
=
a
(
sin
B
)
{\displaystyle \Rightarrow h=b\,(\sin A)=a\,(\sin B)}
⇒
a
sin
A
=
b
sin
B
(
1
)
{\displaystyle \Rightarrow {\frac {a}{\sin A}}={\frac {b}{\sin B}}\,\,\,(1)}
ដូចគ្នាដែរចំពោះកំពស់គូសចេញពីកំពូល A មកជ្រុង BC នៃត្រីកោណ គេបាន
b
sin
B
=
c
sin
C
(
2
)
{\displaystyle {\frac {b}{\sin B}}={\frac {c}{\sin C}}\,\,\,(2)}
(
1
)
{\displaystyle (1)\,}
(
2
)
{\displaystyle (2)\,}
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle \color {blue}{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}}
សំរាយបញ្ជាក់
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=\color {magenta}2R}
គេមានត្រីកោណ ABC ចារឹកក្នុងរង្វង់ កាំ R និង
B
C
=
a
,
∠
A
=
A
{\displaystyle BC=a,\quad \angle A=A}
(ក) - ករណី
0
<
∠
A
<
π
2
{\displaystyle 0<\angle A<{\frac {\pi }{2}}}
ករណីមុំ A ជាមុំស្រួច BD ជាអង្កត់ផ្ចិត នៃរង្វង់ចារឹកក្រៅ ត្រីកោណ នោះចំនុច D គឺស្ថិតនៅលើរង្វង់ ។
នាំអោយ
B
D
=
2
R
{\displaystyle BD=2R\,}
ដោយយោងតាមទ្រឹស្តីបទមុំចារឹកក្នុង រង្វង់ គេបាន
∠
A
=
∠
D
{\displaystyle \angle A=\angle D\,}
BD ជាអង្កត់ផ្ចិត នៃរង្វង់ចារឹកក្រៅត្រីកោណ នោះគេបាន
B
D
=
2
R
,
{\displaystyle {\rm {BD}}=2R,\ }
∠
B
C
D
=
π
2
{\displaystyle \angle {\rm {BCD}}={\pi \over 2}\ }
តាង
∠
B
D
C
=
∠
D
=
D
{\displaystyle \angle {\rm {BDC}}=\angle D=D}
sin
D
=
B
C
B
D
=
a
2
R
⇒
a
sin
D
=
2
R
{\displaystyle \sin D={\frac {BC}{BD}}={a \over 2R}\qquad \Rightarrow {\frac {a}{\sin D}}=2R}
ដោយមុំ D = A គេបាន
a
sin
A
=
2
R
{\displaystyle {a \over \sin A}=2R}
តាមរយៈវិធីដូចគ្នាចំពោះផ្សេងទៀត (មុំ B និងមុំ C) គេបាន
b
sin
B
=
2
R
{\displaystyle {b \over \sin B}=2R}
c
sin
C
=
2
R
{\displaystyle {c \over \sin C}=2R}
ហេតុនេះ
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle \color {magenta}{a \over \sin A}={b \over \sin B}={c \over \sin C}=2R}
សនិដ្ឋាន: ដូចនេះគេបានទ្រឹស្តីបទស៊ីនុស
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle \color {magenta}{a \over \sin A}={b \over \sin B}={c \over \sin C}=2R}
a
=
B
H
+
H
C
=
A
B
⋅
cos
B
+
A
C
⋅
cos
C
=
c
cos
B
+
b
cos
C
⇒
b
=
a
cos
C
+
c
cos
A
⇒
c
=
a
cos
B
+
b
cos
A
{\displaystyle {\begin{aligned}a&=BH+HC\\&=AB\cdot \cos B+AC\cdot \cos C\\&={\color {blue}c\cos B+b\cos C}\\\Rightarrow b&=a\cos C+c\cos A\\\Rightarrow c&=a\cos B+b\cos A\end{aligned}}}
ទ្រឹស្តីបទកូស៊ីនុស
a
2
=
b
2
+
c
2
+
2
b
c
cos
(
B
+
C
)
=
b
2
+
c
2
+
2
b
c
cos
B
cos
C
−
2
b
c
sin
B
sin
C
=
(
b
cos
C
+
c
cos
B
)
2
+
(
b
sin
C
−
c
sin
B
)
2
=
a
2
+
(
b
sin
C
−
c
sin
B
)
2
⇒
b
sin
C
−
c
sin
B
=
0
⟺
b
sin
B
=
c
sin
C
(
i
)
{\displaystyle {\begin{aligned}a^{2}&=b^{2}+c^{2}+2bc\cos {(B+C)}\\&=b^{2}+c^{2}+2bc\cos {B}\cos {C}-2bc\sin {B}\sin {C}\\&=(b\cos {C}+c\cos {B})^{2}+(b\sin {C}-c\sin {B})^{2}\\&=a^{2}+(b\sin {C}-c\sin {B})^{2}\\&\Rightarrow b\sin {C}-c\sin {B}=0\\&\Longleftrightarrow {\frac {b}{\sin {B}}}={\frac {c}{\sin {C}}}\qquad \color {MidnightBlue}(i)\end{aligned}}}
ដូចគ្នាដែរចំពោះ
b
2
=
a
2
+
c
2
+
2
a
c
cos
(
A
+
C
)
⇒
a
sin
A
=
c
sin
C
(
i
i
)
{\displaystyle b^{2}=a^{2}+c^{2}+2ac\cos {(A+C)}\Rightarrow {\frac {a}{\sin {A}}}={\frac {c}{\sin {C}}}\qquad \color {MidnightBlue}(ii)}
c
2
=
a
2
+
b
2
+
2
a
b
cos
(
A
+
B
)
⇒
a
sin
A
=
b
sin
B
(
i
i
i
)
{\displaystyle c^{2}=a^{2}+b^{2}+2ab\cos {(A+B)}\Rightarrow {\frac {a}{\sin {A}}}={\frac {b}{\sin {B}}}\qquad \color {MidnightBlue}(iii)}
ដូចនេះ តាម
(
i
)
,
(
i
i
)
{\displaystyle \color {MidnightBlue}(i),\quad (ii)}
(
i
i
i
)
{\displaystyle \color {MidnightBlue}(iii)}
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle \color {magenta}{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}}
គេមានត្រីកោណ ABC ដែលមានរង្វាស់ជ្រុង a, b, c ចារឹកក្នុងរង្វង់កាំ R ។ ស្រាយបំភ្លឺថាៈ
a
cos
A
+
b
cos
B
+
c
cos
C
=
2
S
R
{\displaystyle a\cos A+b\cos B+c\cos C={\frac {2S}{R}}}
ដែល
S
{\displaystyle S\,}
ក្រលាផ្ទៃនៃត្រីកោណ ABC ។
ដំណោះស្រាយ
តាមទ្រឹស្តីបទស៊ីនុសនៃត្រីកោណ ABC ចារឹកក្នុងរង្វង់ កាំ R
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
⇒
{
a
=
2
R
s
i
n
A
b
=
2
R
s
i
n
B
c
=
2
R
s
i
n
C
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R\Rightarrow {\begin{cases}a=2RsinA\\b=2RsinB\\c=2RsinC\\\end{cases}}}
យើងបាន:
a
c
o
s
A
+
b
c
o
s
B
+
c
c
o
s
C
=
2
R
s
i
n
A
c
o
s
A
+
2
R
s
i
n
B
c
o
s
B
+
2
R
s
i
n
C
c
o
s
C
=
R
(
2
s
i
n
A
c
o
s
A
+
2
s
i
n
B
c
o
s
B
+
2
s
i
n
C
c
o
s
C
)
=
R
(
2
s
i
n
A
c
o
s
A
+
s
i
n
2
B
+
s
i
n
2
C
)
=
R
[
2
s
i
n
A
c
o
s
A
+
2
s
i
n
(
B
+
C
)
c
o
s
(
B
−
C
)
]
=
R
[
2
s
i
n
A
c
o
s
A
+
2
s
i
n
A
c
o
s
(
B
−
C
)
]
(
B
+
C
=
π
−
A
⇒
s
i
n
(
B
+
C
)
=
s
i
n
(
π
−
A
)
=
s
i
n
A
)
=
2
R
s
i
n
A
[
c
o
s
(
B
−
C
)
−
c
o
s
(
B
+
C
)
]
(
A
=
π
−
(
B
+
C
)
⇒
c
o
s
A
=
c
o
s
[
π
−
(
B
+
C
)
]
=
−
c
o
s
(
B
+
C
)
=
2
R
s
i
n
A
⋅
2
s
i
n
B
s
i
n
C
=
4
R
s
i
n
A
⋅
s
i
n
B
s
i
n
C
=
4
R
⋅
a
2
R
⋅
b
2
R
⋅
c
2
R
=
a
b
c
2
R
2
(
1
)
{\displaystyle {\begin{aligned}acosA+bcosB+ccosC&=2RsinAcosA+2RsinBcosB+2RsinCcosC\\&=R(2sinAcosA+2sinBcosB+2sinCcosC)\\&=R(2sinAcosA+sin2B+sin2C)\\&=R[2sinAcosA+2sin(B+C)cos(B-C)]\\&=R[2sinAcosA+2sinAcos(B-C)]\\&(B+C=\pi -A\Rightarrow sin(B+C)=sin(\pi -A)=sinA)\\&=2RsinA[cos(B-C)-cos(B+C)]\\&(A=\pi -(B+C)\Rightarrow cosA=cos[\pi -(B+C)]=-cos(B+C)\\&=2RsinA\cdot 2sinBsinC\\&=4RsinA\cdot sinBsinC\\&=4R\cdot {\frac {a}{2R}}\cdot {\frac {b}{2R}}\cdot {\frac {c}{2R}}\\&={\frac {abc}{2R^{2}}}\,\,\,\,(1)\\\end{aligned}}}
S
{\displaystyle \ S}
កាំ R
⇒
S
=
a
b
c
4
R
⇒
a
b
c
=
4
R
S
{\displaystyle \Rightarrow S={\frac {abc}{4R}}\Rightarrow abc=4RS}
ជំនួស abc ក្នុង
(
1
)
{\displaystyle (1)\,}
a
c
o
s
A
+
b
c
o
s
B
+
c
c
o
s
C
=
4
R
S
2
R
2
=
2
S
R
{\displaystyle acosA+bcosB+ccosC={\frac {4RS}{2R^{2}}}={\frac {2S}{R}}}
ដូចនេះ
a
c
o
s
A
+
b
c
o
s
B
+
c
c
o
s
C
=
2
S
R
{\displaystyle acosA+bcosB+ccosC={\frac {2S}{R}}}
[ កែប្រែ ] ត្រីកោណស្វ៊ែរ ABC គេមានត្រីកោណស្វ៊ែរ ABC ស្ថិតនៅលើស្វ៊ែរ ដែលមានផ្ចិត O កាំ
ρ
{\displaystyle \rho \,}
sin
a
sin
A
=
sin
b
sin
B
=
sin
c
sin
C
=
6
V
O
A
B
C
ρ
3
sin
a
sin
b
sin
c
{\displaystyle {{\sin a} \over {\sin A}}={{\sin b} \over {\sin B}}={{\sin c} \over {\sin C}}={\frac {6V_{\mathrm {OABC} }}{\rho ^{3}\sin a\,\sin b\,\sin c}}}
ដែល
α
=
∠
A
{\displaystyle \alpha =\angle A\,}
β
=
∠
B
{\displaystyle \beta =\angle B\,}
γ
=
∠
C
{\displaystyle \gamma =\angle C\,}
V
O
A
B
C
{\displaystyle V_{\mathrm {OABC} }\,}
មាឌ នៃតេត្រាអែត OABC ។



























































![{\displaystyle {\begin{aligned}acosA+bcosB+ccosC&=2RsinAcosA+2RsinBcosB+2RsinCcosC\\&=R(2sinAcosA+2sinBcosB+2sinCcosC)\\&=R(2sinAcosA+sin2B+sin2C)\\&=R[2sinAcosA+2sin(B+C)cos(B-C)]\\&=R[2sinAcosA+2sinAcos(B-C)]\\&(B+C=\pi -A\Rightarrow sin(B+C)=sin(\pi -A)=sinA)\\&=2RsinA[cos(B-C)-cos(B+C)]\\&(A=\pi -(B+C)\Rightarrow cosA=cos[\pi -(B+C)]=-cos(B+C)\\&=2RsinA\cdot 2sinBsinC\\&=4RsinA\cdot sinBsinC\\&=4R\cdot {\frac {a}{2R}}\cdot {\frac {b}{2R}}\cdot {\frac {c}{2R}}\\&={\frac {abc}{2R^{2}}}\,\,\,\,(1)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f501b3dc25d9bd8b7d2879acf63d446dd65a197)










